Теперь уже все готово для того, чтобы с помощью выражения (6.1) подсчитать вероятность P (k, n) выпадения k раз «орла» в серии из n испытаний. Полное число всех возможностей будет 2n (поскольку в каждом испытании возможны два исхода), а число равновероятных комбинаций, в которых выпадет «орел», будет
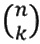, так что
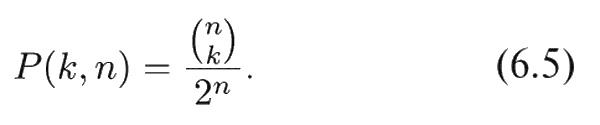
Поскольку P (k, n) – доля тех серий испытаний, в которых выпадение «орла» ожидается k раз, то из ста серий k выпадений «орла» ожидается 100 P (k, n) раз. Пунктирная кривая на фиг. 6.2 проведена как раз через точки функции 100 P (k, 30). Видите, мы ожидали получить 15 выпадений «орла» в 14 или 15 сериях испытаний, а получили только в 13. Мы ожидали получить 16 выпадений «орла» в 13 или 14 сериях испытаний, а получили в 16. Но такие флуктуации вполне допускаются «правилами игры».
Использованный здесь метод можно применять и в более общей ситуации, где в каждом единичном испытании возможны только два исхода, которые давайте обозначим через В (выигрыш) и П (проигрыш). Вообще говоря, вероятности В и П в каждом отдельном испытании могут быть разными. Пусть р, например, будет вероятностью результата В. Тогда q (вероятность результата П) должна быть равна (1 – p). В серии из n испытаний вероятность того, что результат В получится k раз, равна
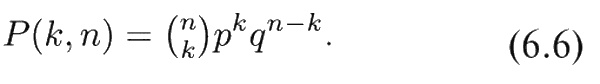
Эта функция вероятностей называется биномиальным законом распределения вероятности.
§ 3. Случайные блуждания
Существует еще одна интересная задача, при решении которой не обойтись без понятия вероятности. Это проблема «случайных блужданий». В простейшем варианте эта задача выглядит следующим образом. Вообразите себе игру, в которой игрок, начиная от точки х = 0, за каждый ход может продвинуться либо вперед (до точки х), либо назад (до точки – х), причем решение о том, куда ему идти, принимается совершенно случайно, ну, например, с помощью подбрасывания монеты. Как описать результат такого движения? В более общей форме эта задача описывает движение атомов (или других частиц) в газе – так называемое броуновское движение – или образование ошибки при измерениях. Вы увидите, насколько проблема «случайных блужданий» тесно связана с описанным выше опытом с подбрасыванием монеты.
Прежде всего давайте рассмотрим несколько примеров случайных блужданий. Их можно описать «чистым» продвижением Dn за N шагов. На фиг. 6.5 показаны три примера путей при случайном блуждании.
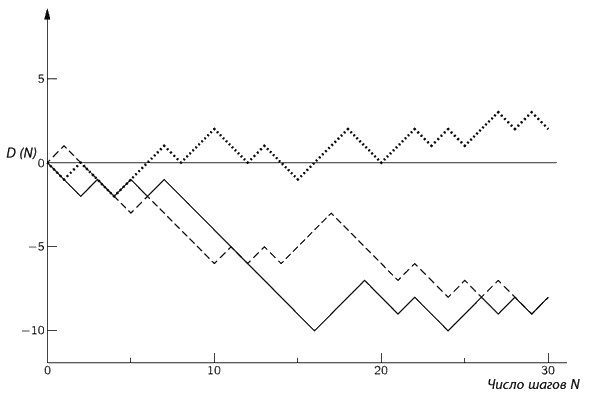
Фиг. 6.5. Три примера случайного блуждания. По горизонтали отложено число шагов N, по вертикали – координата D(N), т. е. чистое расстояние от начальной точки.
(При построении их в качестве случайной последовательности решений о том, куда сделать следующий шаг, использовались результаты подбрасывания монеты, приведенные на фиг. 6.1.)
Что можно сказать о таком движении? Ну, во-первых, можно спросить: как далеко мы в среднем продвинемся? Нужно ожидать, что среднего продвижения вообще не будет, поскольку мы с равной вероятностью можем идти как вперед, так и назад. Однако чувствуется, что с увеличением N мы все с большей вероятностью можем блуждать где-то всё дальше и дальше от начальной точки. Поэтому возникает вопрос: каково среднее абсолютное расстояние, т. е. каково среднее значение |D|? Впрочем, удобнее иметь дело не с |D|, а с D 2; эта величина положительна как для положительного, так и для отрицательного движения и поэтому тоже может служить разумной мерой таких случайных блужданий.
Можно показать, что ожидаемая величина D 2N равна просто N – числу сделанных шагов. Кстати, под «ожидаемой величиной» мы понимаем наиболее вероятное значение (угаданное наилучшим образом), о котором можно думать как об ожидаемом среднем значении большого числа повторяющихся процессов блуждания. Эта величина обозначается как <D 2N> и называется, кроме того, «средним квадратом расстояния». После одного шага D2 всегда равно +1, поэтому, несомненно, <D 21> = 1. (За единицу расстояния всюду будет выбираться один шаг, и поэтому я в дальнейшем не буду писать единиц длины).
Ожидаемая величина D 2N для N > 1 может быть получена из DN − 1. Если после (N − 1) шагов мы оказались на расстоянии DN − 1, то еще один шаг даст либо DN = DN − 1 + 1, либо DN = DN − 1 − 1. Или для квадратов
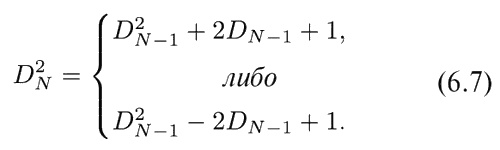
Если процесс повторяется большое число раз, то мы ожидаем, что каждая из этих возможностей осуществляется с вероятностью 1/2, так что средняя ожидаемая величина будет просто средним арифметическим этих значений, т. е. ожидаемая величина D 2N будет просто D 2N − 1 + 1. Но какова величина D 2N − 1, вернее, какого значения ее мы ожидаем? Просто, по определению, ясно, что это должно быть «среднее ожидаемое значение» <D 2N − 1>, так что
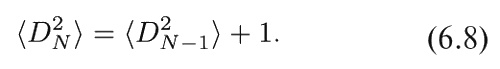
Если теперь вспомнить, что <D 21> = 1, то получается очень простой результат:
Отклонение от начального положения можно характеризовать величиной типа расстояния (а не квадрата расстояния); для этого нужно просто извлечь квадратный корень из D < 2N > и получить так называемое среднее квадратичное расстояние DСК:
