Мы изучаем такие методы, как счет, чтобы сформировать концепцию числа — представление о нем. Мы осваиваем метод продолжения счета, чтобы воспринять концепцию суммы, а усвоив метод многократного сложения, мы поймем концепцию произведения.
Математика — концептуальный предмет, но многие ученики не видят ее в таком ракурсе. Математика для них — это набор правил или методов, которые нужно запомнить. Как мы уже обсуждали, такой подход становится в итоге серьезной проблемой, и некоторые исследования мозга проливают свет на причины, по которым это происходит.
Когда вы изучаете область, о которой ничего не знаете, она занимает много места в вашем мозге: ведь вам нужно напряженно размышлять, как это работает и как разные концепции соотносятся друг с другом. Но математические понятия, которые вы изучили ранее и хорошо знаете (например, сложение), занимают в мозге небольшое пространство. Вы можете использовать эти знания, даже не задумываясь. Процесс сжатия происходит потому, что головной мозг — крайне сложный орган, контролирующий много разных процессов, и в один момент он может сосредоточиться только на нескольких несжатых концепциях. Те же, которые вы хорошо знаете, сжимаются и архивируются. Уильям Тёрстон, выдающийся математик, получивший Филдсовскую премию, так описывает процесс сжатия.
Математика поразительно легко поддается сжатию: вы можете долго и напряженно трудиться, шаг за шагом прорабатывая один процесс или идею с нескольких точек зрения. Но как только вы по-настоящему поймете нечто и сможете увидеть это как единое целое, скорее всего, произойдет очень сильное ментальное сжатие. Вы можете отправить эту информацию в архив, а при необходимости быстро и полностью восстановить и использовать ее всего лишь за один шаг в рамках другого ментального процесса. Озарение, которым сопровождается такое сжатие, — одна из истинных радостей
[129].
Многие ученики не считают, что математика дарит подлинную радость, — отчасти потому, что в их мозге сжатия не происходит. Мозг способен сжимать только концепции, но не правила и методы. Следовательно, у учеников, которые не мыслят концептуально, а воспринимают математику как список правил, подлежащих запоминанию, сжатия не происходит и их мозг не может упорядочивать концепции и архивировать их, а пытается хранить длинные списки методов и правил
[130]. Вместо сжатых концепций их знания больше напоминают лестницу, состоящую из нагромождения заученных методов и, как им кажется, ведущую наверх. Именно поэтому важно воспитать концептуальный подход к математике — основу математического мышления.
Когда я рассказываю учителям и родителям об этом исследовании, они задают вопрос: «Как сделать так, чтобы мои ученики воспринимали информацию концептуально?» Существует много способов научить детей размышлять на концептуальном уровне. Во-первых, важно донести до них причины, почему работают те или иные методы, а не просто предлагать заучивать их. В предыдущей главе мы говорили о том, насколько важно задавать ученикам вопросы об их видении той или иной идеи и убеждать их в том, что это действительно способствует ее концептуальному пониманию.
Еще один концептуальный подход к преподаванию и изучению математики, названный «Беседы о числах», был задуман преподавателями Рут Паркер и Кэти Ричардсон и разработан Кэти Хамфриз и Шерри Пэрриш. Метод состоит в обсуждении чисел и позволяет ученикам младших и средних классов развивать чувство числа и понимать гибкую и концептуальную природу математики. В ходе обсуждений ученикам предлагают совершить вычисления в уме, не используя бумагу и ручку. Затем учителя собирают информацию о том, какие методы счета использовали ученики.
Обучая других проводить беседы о числах, я, помимо прочего, рекомендую применять визуальные решения, чтобы активировать разные нейронные связи в мозге. Чтобы понять это, попробуйте вычислить в уме, сколько будет 18 × 5, до того как вы прочитаете или подсмотрите пути решения.
На рис. 5.4 приведены шесть разных способов вычисления 18 × 5 (на самом деле их больше) с визуальными решениями.
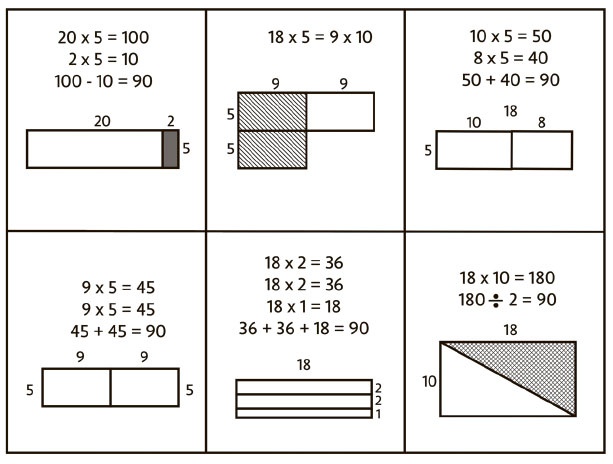
Рис. 5.4. Шесть визуальных решений задачи на умножение
Можно обозначить все проблемы с числами и решать их по-разному, разбивая числа на суммы или произведения и приводя к более «удобным» для счета числам, например 20, 10, 5 или 100. Это упрощает вычисления и способствует гибкости в обращении с числами, лежащей в основе чувства числа. Ученики любят рассказывать о своих стратегиях; как правило, они увлеченно и с интересом анализируют разные методы, используемые при решении задач. Они осваивают ментальную математику, у них появляется возможность запомнить факты, а также формируется концептуальное понимание чисел и арифметических свойств, что крайне важно для успешного изучения алгебры и других разделов математики.
Когда я продемонстрировала разные подходы к решению одной задачи, многие были удивлены и испытали чувство освобождения.
Однажды меня пригласили на встречу с удивительным человеком — профессором Стэнфордского университета Себастьяном Труном и его командой в Udacity
[131], занимающейся дистанционным образованием. Трун руководил разработкой беспилотных автомобилей и был одним из первых создателей открытых онлайн-курсов (Massive Open Online Courses, MOOCs). В настоящее время он разрабатывает летающие автомобили. Я взяла у него интервью для своего первого онлайн-курса, адресованного учителям, чтобы распространить его идеи о математике и преподавании.
Себастьян пригласил меня в Udacity пообщаться с его командой. Тогда мы и познакомились. В тот день я сидела в многолюдной комнате вместе с инженерами. Те, кто втиснулся в небольшое помещение, сидели вокруг стола, остальные расположились на полу вдоль стен. Себастьян представил меня собравшимся и тут же начал забрасывать вопросами о правильных подходах к изучению математики. А я спросила присутствующих, не хотят ли они все вместе решить математическую задачу. Они охотно согласились. Я попросила их найти произведение 18 × 5, затем собрала методы счета, разыграв мини-версию бесед о числах. В тот день для решения примера было использовано шесть разных методов, и я нарисовала их на столе, вокруг которого мы сидели. Вся группа была настолько поражена, что некоторые поспешили на улицу и стали предлагать прохожим посчитать, сколько будет 18 × 5. Впоследствии они записали небольшой онлайн-курс по решению этого примера и изготовили футболки с надписью «18 × 5», которые носили в Udacity.



