Когда Нэнси составила пособия для визуального решения математических задач и объяснила ученикам, почему мы это делаем, а не как это сделать, то Милли впервые справилась с заданием и, сделав это однажды, продолжала двигаться дальше. В результате постепенно избавилась от ложного представления о том, что никогда не сможет успевать по математике.
Нэнси старалась работать так, чтобы все ученики в ее классе и других классах школы приобрели положительный опыт в изучении математики. Среди ее учеников были и те, кто поставил на себе крест, и она делала все возможное, чтобы изменить их представление о себе. Нэнси дала Милли домашнее задание, которое помогло девочке посмотреть на математику с другой стороны. Во время школьных тестов она сидела рядом с Милли и показывала ей, как можно найти решение с помощью визуальных инструментов. До того как девочка попала в класс к Нэнси, по математике ей ставили только D и F. По итогам учебного года Милли получила оценку B. Но более важным оказалось то, что она начала понимать материал и больше не считала себя неспособной к математике.
Нэнси проработала со всеми учителями идеи, которые легли в основу и этой книги, и книги «Математическое мышление»
[127], и моих онлайн-уроков. Размышляя о произошедших в школе переменах, она написала:
Я не думала, что когда-нибудь мне повезет увидеть группу учителей, настолько увлеченных работой с детьми и преподаванием математики. И мне не терпится увидеть перемены в их учениках. Это касается не только моего класса или какого-то одного ученика, но и других детей, а также многих учителей, которым пошли на пользу перемены, повлиявшие на их повседневную жизнь.
Удивительная история о том, как благодаря усилиям учителя изменилась не только сама Милли, но и ее взгляды и подход к жизни, выявляет способы, с помощью которых ученики могут преодолеть ограничения и снять их. Чтобы лучше понять эту теорию, мы намерены глубже погрузиться в изучение математики. В помощь нам будут результаты захватывающего исследования, которые вне зависимости от изучаемого предмета содержат важные выводы для учителей и учащихся, а также для родителей и руководителей. Данное исследование позволяет понять принцип работы человеческого мозга и роль гибкости мышления.
Гибкое мышление
Профессора британского Уорикского университета Эдди Грей и Дэвид Толл работали с учениками в возрасте от 7 до 13 лет. Учителя отнесли их к числу слабых, середнячков и сильных
[128]. Исследователи давали ученикам арифметические задачи, показывали визуальные решения, а затем анализировали, какими способами школьники получили результат. Так, в примере 7 + 19 числа были представлены визуально (см. рис. 5.2).
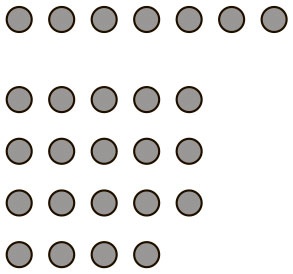
Рис. 5.2. Визуальное представление сложения двух чисел — 7 и 19.
Ученые обнаружили, что разница между сильными и слабыми учениками состояла не в том, что первые знали больше. Сильные школьники решали задачи с помощью так называемого чувства числа — их работа носила гибкий и концептуальный характер. Исследователи выделили два метода подсчета: в рамках метода «считаем всё» дети просто считали, сколько в первом множестве, сколько во втором и потом складывали первое со вторым; метод «продолжение счета» используется, когда заданы два числа (например, 15 и 4). В этом случае сложение осваивается так: сначала дети считают до 15, а затем продолжают счет — 16–17–18–19. Изучая метод продолжения, ученики усваивают понятие суммы. Речь не о методе сложения, а о самой идее. Знание математических фактов проявлялось тогда, когда испытуемые помнили их, а чувство числа — в случаях, когда они гибко оперировали числами, например решали задачу на сложение 7 + 19, упрощая ее и вычисляя сумму 6 + 20. Ниже приведены методы, которыми пользовались сильные и слабые ученики.
Сильные ученики:
30% — знание математических фактов;
9% — метод продолжения счета;
61% — чувство числа.
Слабые ученики:
6% — знание математических фактов;
72% — метод продолжения счета;
22% — метод «считаем всё»;
0% — чувство числа.
Результаты оказались впечатляющими. Сильные ученики мыслили гибко; у 61% из них проявилось чувство числа. Слабые вообще не обращались к чувству числа. Они применяли другие методики счета, например продолжение счета или обратный счет (начиная с какого-то одного числа и считая в обратном порядке), причем придерживались формальных схем даже в тех случаях, когда это не имело смысла. Исследователи высказали важное соображение: слабые ученики, не отличавшиеся гибкостью мышления, изучали другую математику, более сложную. Это проиллюстрировали с помощью задачи на вычитание: 16–13.
Слабые ученики решали ее с помощью обратного счета, то есть выбирали более трудный путь (попробуйте-ка начать с 16 и отсчитать 13 чисел в обратном порядке); при этом вероятность ошибки довольно высока. Сильные ученики действовали гибко, вычитая 3 из 6 и 10 из 10, получали ответ 3. Подобная гибкость в обращении с числами предельно важна, но если учеников обучают слепо заучивать математические факты и применять математические методы без понимания их сути, то они автоматически обращаются к тому, что вызубрили, и никогда не разовьют способность концептуально размышлять о числах и гибко взаимодействовать с ними.
Часто с отстающими учениками начальной школы занимаются дополнительно и отдельно от других, особенно если у них проблемы со счетом, — подход под названием «тренировать и готовить» сами ученики метко переименовали в «тренировать и убивать». Это последнее, что им нужно. Такие ученики не успевают по математике из-за неправильного подхода к обучению, думая, что им необходимо опираться на запоминание. Даже в тех случаях, когда чувство числа принесло бы им больше пользы, они продолжают применять методы счета, основанные на заучивании. Вместо того чтобы заниматься зубрежкой, им необходимо научиться гибко и творчески обращаться с числами. Они должны подходить к числам по-другому — концептуально.
Концептуальное обучение
Что это значит — подходить к числам концептуально? Многим читателям, кому внушали, что нужно запоминать математические методы и факты, это может показаться чужеродной идеей. Грей и Толл разграничили концепции и методы (рис. 5.3).
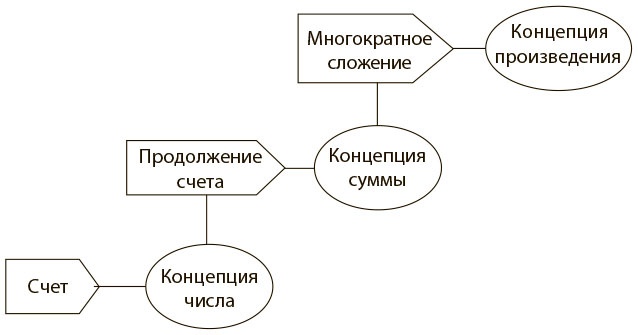
Рис. 5.3. Математические методы и концепции




