1.145. Примеры расширения при взрыве
Однажды профессор Джонс из Абердинского университета
[22] вышел на улицу и увидел стакан воды. В руке у него случайно оказался пистолет, и ради развлечения он выстрелил в стакан, ожидая, что тот разлетится на множество осколков, как случается с пустым стаканом, когда в него попадает пуля. Вместо этого стакан с водой исчез. Позже он объяснял на своих лекциях, почему это случилось.
Через несколько лет инженеры из Королевского инженерного корпуса в Абердине решили снести высокую заводскую трубу, воспользовавшись для этого лекциями профессора Джонса, объяснявшими физику этого процесса. Они заложили взрывчатку на дно кирпичной трубы, затем заполнили трубу на два метра водой, рассчитывая, что взрыв разрушит фундамент и труба упадет на землю. Они оказались правы лишь наполовину. Нижние два метра трубы смело взрывом, да так аккуратно, что верхняя часть трубы осела и прочно встала прямо на обломки старого основания. И инженеры оказались перед еще более трудной задачей.
Почему и стакан, и нижние два метра трубы полностью уничтожило взрывом?
Серия потрясающих стробоскопических (последовательно снятых с короткими выдержками) фотографий доктора Эджертона из Массачусетского технологического института запечатлела то, что происходит с обычной лампочкой, когда в нее попадает пуля. Когда пуля проникает в колбу лампы, стекло в пулевом отверстии превращается в пыль, а потом небольшая часть этой пыли летит обратно в сторону пистолета, из которого был произведен выстрел. Разве из рассмотрения сил и импульсов не следует вывод о том, что пыль должна лететь исключительно туда же, куда и пуля?
ОТВЕТ • Когда пуля попадает в пустой стакан, стекло вокруг входного и выходного отверстий рассыпается в пыль, вдоль стенок стакана бегут трещины, и остальное стекло разлетается на осколки. Если стакан наполнен водой, жидкость не может освободить место для летящей пули и сопровождающей ее ударной волны. Поэтому вода расширяется и толкает стенки стакана, разбивая их в пыль, так что мельчайшие частички летят во всех направлениях. То же происходит и с кирпичами, расположенными в нижней части трубы на высоте до двух метров, когда веществам, образовавшимся при взрыве, внезапно требуется дополнительное пространство.
Распыленное стекло, летящее назад в демонстрациях Эджертона, тоже уносилось расширившимся газом, небольшое количество которого содержалось в колбе лампы.
1.146. Почему висящая на стене картина перекашивается?
Если вы повесите картину на короткой веревке на гвоздь, есть вероятность, что она со временем перекосится. Из-за чего ее положение неустойчиво? Можно ли ее как-нибудь уравновесить, не привязывая к гвоздю и не вешая на два вбитых на некотором расстоянии друг от друга гвоздя?
ОТВЕТ • Если веревка короткая, картина находится в неравновесном состоянии и любое случайное возмущение приведет к тому, что она перекосится — ведь в таком положении центр ее масс опустится. Можно уменьшить эту неустойчивость, подвесив картину на более длинной веревке. Минимальная длина веревки определяется соотношением между углом, образованным двумя отрезками веревки с гвоздем в качестве вершины, и боковым углом между диагоналями самой картины (рис. 1.47). Когда угол между диагоналями меньше, чем угол между отрезками веревки на гвозде, картина висит нестабильно. Когда вы заменяете веревку на более длинную, вы уменьшаете угол между отрезками веревки. Когда он становится меньше угла между диагоналями, при перекашивании центр масс картины не может опуститься, так что она останется висеть в прежнем положении.
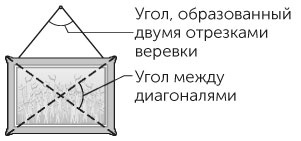
Рис. 1.47 / Задача 1.146. Углы, определяющие положение повешенной на стену картины.
1.147. Фокус с двумя пружинами
Найдите две пружины с примерно одинаковой длиной и упругостью и с помощью их и трех кусков веревки подвесьте груз, как показано на рис. 1.48. Один из кусков веревки связывает концы пружин и поэтому натянут. Два других куска имеют одинаковую длину, но она больше, чем нужно, чтобы поддерживать блок, поэтому веревки висят свободно и образуют петли.
Куда устремится груз — вверх или вниз, — если перерезать короткий кусок веревки, соединяющий пружины, и блок повиснет на длинных веревках?
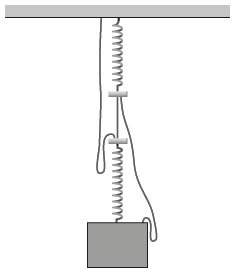
Рис. 1.48 / Задача 1.147. Груз, висящий на двух пружинах и трех веревках, две из которых свободно свисают.
ОТВЕТ • Когда вы перережете короткую веревку, новое положение груза будет определяться двумя противоположными тенденциями. Одна связана с тем, что он теперь может держаться на двух более длинных веревках, которые раньше свисали петлями, а теперь натянулись под его воздействием, так что он должен был бы опуститься. Вторая связана с тем, что в начальной конструкции каждая пружина выдерживала полный вес груза, а в новой конфигурации на каждую из них должна прийтись лишь половина этого веса. Поэтому в новой конфигурации пружины меньше растянуты и, следовательно, груз будет стремиться подняться. При условии, что длинные веревки не слишком длинные, вторая тенденция возобладает, и груз в результате поднимется, а не опустится.
1.148. Устойчивость банки с лимонадом
Устойчивость стоящей на столе жестяной банки с лимонадом или другим напитком зависит от количества энергии, которую нужно затратить на то, чтобы перевести ее из нормального — вертикального — состояния в такое, когда центр ее масс поднимется и окажется в точности над кромкой донышка на столе. Какая банка более устойчива — полная или пустая? Существует ли определенный уровень жидкости в банке, при котором она наиболее устойчива? Этот вопрос может оказаться важным, если банка стоит на столике в самолете, попавшем в зону турбулентности, или если ее подтолкнуть так, чтобы она скользила по столу.
ОТВЕТ • Полная банка устойчивее пустой. Хотя центр масс в обоих случаях находится почти на середине ее высоты, большая масса наполненной банки означает, что для того, чтобы наклонить банку на такой угол, когда она опрокинется, требуется большая энергия.
Если вы станете медленно сливать жидкость из банки, на ее устойчивость повлияют три фактора. Центр масс будет опускаться до тех пор, пока уровень жидкости не опустится до середины, а потом начнет опять подниматься. Масса жидкости будет уменьшаться по мере ее выливания. Из наклоненной банки жидкость вытекает так, что ее верхняя поверхность остается горизонтальной. Учитывая все эти факторы, получаем, что обычная банка с жидкостью устойчивее всего, когда высота ее содержимого чуть больше радиуса банки.




