Если вы кантуете лыжи, наклоняя корпус вперед, они врезаются в снег, и трение в передней части лыжи увеличивается, а в задней — уменьшается (рис. 1.35в). В этом случае вращающий момент, действующий на переднюю часть лыжи, преобладает, и вы поворачиваете налево.
Край (кант) лыж для слалома слегка искривлен, чтобы было легче поворачивать. Когда вы вдавливаете этот кант в снег и скользите по траектории, являющейся продолжением искривленного края лыжи, трение будет минимальным.
На коротких лыжах так сильно подбрасывает на неровной поверхности, что можно легко потерять равновесие. Хотя длинными лыжами труднее управлять, на них подбрасывает меньше.
Чтобы понять, почему нужно наклоняться вперед при спуске по линии спада, представьте себе, что вес лыжника — это вектор, проведенный через центр его масс. Вектор можно разложить на две составляющие (компоненты). Одна компонента направлена вниз по склону (она ответственна за движение лыжника), а вторая перпендикулярна ему. Чтобы лыжник не потерял равновесия, этот перпендикуляр должен проходить через ступни спортсмена. А если лыжник решит на спуске не наклоняться, возникнет вращающий момент относительно ступней, который может опрокинуть лыжника назад.
Рассмотрим описанную демонстрацию Свинсона с крутящимся колесом и предположим, что трением в этом случае можно пренебречь, то есть будем считать, что участники (колесо — это тоже участник) изолированы от внешних сил, которые могли бы создать вращающий момент. Посмотрим на Свинсона сверху. Поскольку колесо вначале вращалось вокруг горизонтальной оси, вокруг линии, по которой вы смотрите, не может быть вращения, то есть ни колесо, ни Свинсон не имеют углового момента относительно вертикальной оси. Это следствие отсутствия внешних крутящих сил, и такое положение не может измениться. Если Свинсон опускает правую ручку и поднимает левую, сверху можно увидеть, что колесо вращается против часовой стрелки — это значит, что оно приобрело некоторый угловой момент относительно вертикальной оси. Чтобы общий угловой момент остался нулевым, каким он и был вначале, Свинсон должен будет повернуть по часовой стрелке (если смотреть сверху), то есть вправо.
1.101. Как проползти по скользкому льду
Вы просыпаетесь и обнаруживаете, что оказались посреди большого замерзшего пруда и лед такой скользкий, что по нему невозможно не только идти, но и ползти. Как же оттуда выбраться?
Предположим, вы лежите на льду лицом вниз и думаете, как выбраться. Чтобы не замерзнуть окончательно, вам для начала нужно перевернуться на спину. Как же это сделать?
ОТВЕТ • Бросьте ботинок или какой-то другой предмет в любом направлении, и вы сдвинетесь (к сожалению, ненамного) в противоположном. Поскольку трения между вами и льдом нет, общее количество движения — вашего и брошенного ботинка — останется равным нулю. Когда вы сообщаете импульс брошенному предмету, вы приобретаете точно такой же импульс в противоположном направлении.
Те же физические процессы происходят, когда кто-то пытается катнуть шар для боулинга, стоя на роликовых коньках, у которых трение качения мало. Я как-то раз попытался. Коньки подо мной поехали назад, корпус остался на месте, и от падения лицом вниз меня спасло лишь то, что я схватился за человека рядом.
Чтобы перевернуться на очень скользком льду, нужно вытянуть одну руку и аккуратно ударить ею по льду. Хотя между льдом и рукой нет трения, при ударе со стороны льда на руку подействует сила, направленная вверх. Эта сила позволит вам перевернуться на спину.
1.102. Короткая история. Последовательность вращений имеет значение
Если вы пройдете три метра на север, три метра на восток, три метра на запад и три метра на юг, вы вернетесь в ту же самую точку, независимо от того, в какой последовательности вы проделаете эти четыре коротких отрезка пути. (Чтобы иметь возможность проделать все эти эволюции, вы должны находиться не ближе трех метров к любому из полюсов.) С вращением все иначе. Опустите руку вниз ладонью к бедру. Не поворачивая запястье, 1) поднимите руку так, чтобы она была вытянута вперед, 2) в горизонтальной плоскости отведите ее так, чтобы она указывала вправо, и 3) опустите ее вниз так, чтобы она в результате была направлена вдоль туловища. Теперь ладонь направлена вперед. Проделайте все эти движения в обратном порядке — в сторону, вперед, вниз. Тогда рука вернется в исходное положение и будет прижата к бедру. Куда будет направлена ладонь в конце?
1.103. Волчки тоже бывают разные
Почему вращающийся волчок не падает, даже когда он довольно сильно отклоняется от вертикали? Почему некоторые волчки изначально «спят», то есть крутятся, стоя прямо, а другие прецессируют (вершина центральной оси волчка обращается вокруг вертикальной оси, как это показано на рис. 1.36а)? Почему на прецессию часто накладывается нутация — дополнительное вращение оси волчка вокруг конуса с углом, существенно меньшим, чем при прецессии? Существуют ли различные типы нутаций? Почему некоторые вращающиеся волчки сразу опрокидываются, а другие крутятся и крутятся?
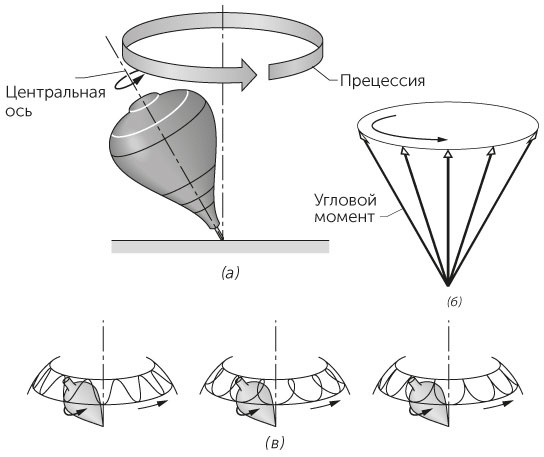
Рис. 1.36 / Задача 1.103. а) Прецессия вращающегося волчка относительно вертикальной оси. б) Вращение вектора углового момента вокруг вертикали. в) Нутация при прецессии.
ОТВЕТ • Обычно когда на тело действует сила, оно движется в направлении этой силы. Но когда тело еще и вращается, приложенная сила может вызвать его движение в перпендикулярном этой силе направлении. Такое движение кажется невозможным, и поэтому волчки (и гироскопы вообще) так интересны. Даже если ребенок еще не знаком с физическими законами, он знает, что наклонившийся волчок должен сразу же упасть, а не прецессировать.
Традиционно прецессию объясняют угловым моментом волчка, который зависит от скорости его вращения вокруг длинной оси. Угловой момент — вектор, направленный вдоль этой оси. Представьте себе мгновенный снимок волчка, вращающегося с большой скоростью против часовой стрелки, если смотреть сверху, и наклонившегося под каким-то углом. На рис. 1.36б угловой момент волчка представлен вектором, направленным по центральной оси вверх.
Из-за того, что сила тяжести, действующая на волчок, направлена вниз, она создает вращающий момент, стремящийся повернуть волчок относительно точки соприкосновения его с полом, в результате чего волчок должен упасть. Однако поскольку волчок вращается и уже обладает угловым моментом, этот вращающий момент только меняет направление углового момента, поворачивая вектор вокруг точки опоры, при этом сам вектор движется по поверхности конуса. Поскольку угловой момент направлен вдоль центральной оси волчка, центральная ось движется по той же поверхности.
Как только волчок запустили, он начинает наклоняться, а его центр масс немного опускается. При этом должны выполняться два закона сохранения: угловой момент волчка относительно вертикальной оси и его полная энергия должны оставаться постоянными. Поскольку опускание центра масс приводит к отклонению оси вращения от вертикали, скорость прецессии должна быть достаточно высока, чтобы полный угловой момент оставался постоянным. Вследствие опускания центра масс потенциальная энергия переходит в кинетическую.

