Похожая бомба, но меньших размеров и сферической формы, была разработана для потопления судов. Две такие бомбы, вращающиеся со скоростью 1000 об./мин, планировалось сбросить с высоты 8 м на расстоянии 1,5 км от цели. Идея заключалась в том, что они будут двигаться к цели по водной поверхности прыжками, как летучие рыбы, и по пути перепрыгивать через противоторпедные сети и другие препятствия. Предполагалось, что, столкнувшись с корпусом корабля, они начнут катиться по нему вниз, пока на заранее выставленной глубине не взорвется 300-килограммовый заряд. Эта бомба была способна проникать и в длинные тоннели: если ее сбросить у входа, она могла бы ускакать вглубь тоннеля и там взорваться. По разным причинам эти маленькие бомбы так никогда и не были использованы. (Физика — наука невероятно интересная, но ее применение может быть очень страшным.)
1.94. Вращение на льду
Выполняющий вращение фигурист — типичный пример для иллюстрации закона сохранения углового момента. Поскольку на него не действуют никакие моменты внешних сил, никакие его действия не могут изменить его угловой момент. А скорость его вращения увеличивается, когда он прижимает руки, из-за того, что он изменил положение части своей массы (рук, а, возможно, и одной ноги) по отношению к оси, вокруг которой крутится. Все это, конечно, правильно, но остается вопрос, какая сила заставляет его крутиться быстрее и почему его кинетическая энергия возрастает?
ОТВЕТ • Если рассматривать движение в инерциальной системе отсчета, связанной со зрителями на трибунах, то изменение скорости вращения фигуриста вызывается внутренними силами взаимодействия различных частей его тела. Когда фигурист прижимает руки к туловищу, линейная скорость рук должна уменьшиться. Следовательно, на них со стороны туловища действуют силы. В свою очередь, руки действуют на туловище, благодаря чему скорость его вращения увеличивается.
1.95. Вращение книги
Стяните обложку тугой резинкой, чтобы книга не раскрылась. Подбросьте книгу в воздух и одновременно закрутите вокруг одной из трех основных осей, как это показано на рис. 1.34а. Вращение вокруг двух из трех осей устойчиво. Почему книга начинает заметно болтаться при вращении вокруг третьей оси? Такую же нестабильность можно заметить, если подбросить в воздух молоток, теннисную ракетку или любой другой предмет.
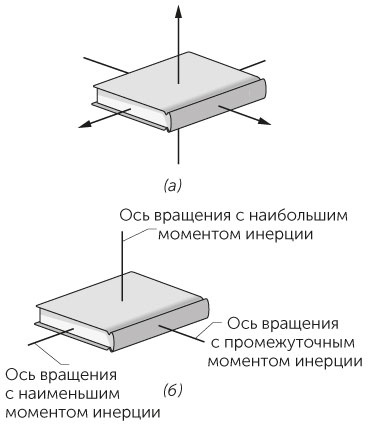
Рис. 1.34 / Задача 1.95. а) Три оси, проведенные через книгу. б) Моменты инерции, связанные с этими осями.
ОТВЕТ • Оси, проведенные через книгу, характеризуются разными связанными с ними моментами инерции, то есть разным распределением массы по отношению к соответствующим осям вращения. При вращении вокруг одной оси масса распределена далеко от оси (момент инерции наибольший), при вращении вокруг другой — масса сосредоточена вблизи этой оси (момент инерции наименьший) (см. рис. 1.34б). При вращении вокруг любой из этих осей вращение стабильно.
Проблемная ось — та, распределение масс вокруг которой, а следовательно, и момент инерции, имеет промежуточное значение. Если вы подкинете и раскрутите книгу в точности вокруг этой оси, она будет вращаться стабильно. Но проблема в том, что подбросить идеально невозможно — вы обязательно ошибетесь, и ошибка приведет к колебаниям, амплитуда которых будет нарастать. По одной из версий, ошибка в начальном расположении приводит к появлению заметной центробежной силы (направленной наружу), которая вынудит книгу вращаться вокруг оси, относительно которой момент инерции максимален. Беспорядочное движение книги, которое вы видите вначале, — это комбинация вращения, которое вы намеревались придать книге, и дополнительного вращения, вызванного центробежной силой.
Проблемная ось с промежуточным моментом инерции существует у всех предметов. Однако если моменты инерции относительно каких-то двух осей равны, вращение вокруг любой из осей будет нестабильным, и это вращение может представлять собой медленный поворот вокруг оси, а не заметные колебания. Кроме того, если сопротивление воздуха при вращении объекта значительно, становится нестабильным и вращение вокруг оси с максимальным моментом инерции. Чтобы проверить этот эффект, подкиньте игральную карту в воздух, закрутив ее вокруг оси с наибольшим моментом инерции. Есть вероятность, что в конце она будет вращаться вокруг оси с наименьшим моментом инерции.
1.96. Падающая кошка, кувырки космонавтов и акробатические прыжки в воду с вышки
Если кошка будет падать спиной вниз с высоты более одного метра, она быстро переориентируется и приземлится на лапы. Может показаться, что такое действие нарушает железобетонное правило физики: если на тело не действует момент внешней силы, угловой момент тела измениться не может. Кошка как раз и есть такое тело. В начале падения у нее нет углового момента, нет и момента сил, заставляющего ее вращаться. Тем не менее она своим вращением как будто доказывает, что ее угловой момент не остается равным нулю. Кошка и правда нарушает закон физики?
Как может космонавт в движущемся по орбите космическом корабле поворачиваться влево или вправо (вращение вокруг вертикальной оси), не опираясь ни на что? Как может космонавт вращаться вокруг горизонтальной оси, идущей слева направо? Может ли он вращаться вокруг горизонтальной оси, идущей спереди назад? Во всех этих случаях тело изначально не вращается и нет также момента внешних сил, действующих на него, а тем не менее космонавт как-то ухитряется поворачиваться.
Прыжки в воду с вышки или трамплина — это другая история, поскольку прыгун в начале прыжка обычно уже имеет угловой момент, который он приобретает, отталкиваясь от твердой поверхности. В простейшем прыжке спортсмен переворачивается в воздухе так, чтобы первыми в воду вошли руки. Быстрое вращение прыгуну нужно, если он хочет несколько раз перевернуться, прежде чем войти в воду. Почему скорость вращения спортсмена возрастает, если он сгруппируется, перед тем как, выпрямившись, войти в воду?
Как прыгун может еще и поворачиваться вокруг другой своей оси во время прыжка в воду? Например, спортсмен может включить три оборота вокруг своей оси в прыжок полтора сальто вперед. Нужно ли как-то по-особому отталкиваться от трамплина для того, чтобы сделать поворот, или прыгун толкается так же, как при обычном сальто, а поворот совершает уже в воздухе? Многие приемы, используемые прыгунами, взяты на вооружение другими спортсменами — фристайлерами (проделывающими фантастические трюки в воздухе), гимнастами, скейтбордистами.
Некоторые прыжки в воду и прыжки с трамплина напоминают падение кошки в том смысле, что и кошка, и спортсмен начинают свой полет с нулевым угловым моментом. Но каким-то чудом без закручивающего его толчка от поверхности прыгун в воду или фристайлер умудряется повернуться во время полета в воздухе.
ОТВЕТ • Объяснениям того, как кошка умудряется переворачиваться в воздухе, уже около ста лет, но до сих пор в них встречаются противоречия. Я приведу две теории падения (в поддержку каждой существуют фотодоказательства), но имейте в виду, что кошки не изучают физику, поэтому не все они прыгают одинаково.

