Теперь рассмотрим ситуацию с игрушкой из нескольких шариков. Фокусы с игрушкой с подвешенными рядышком шариками-маятниками обычно описывают, рассматривая импульс и кинетическую энергию шариков. Единственная возможность для этих величин остаться постоянными при серии соударений — чтобы последний шарик закончил процесс, получив всю первоначальную кинетическую энергию и импульс. Таким образом, в конце он двигается один. Объяснение настолько просто, что сбивает с толку, ведь реальное движение промежуточных шариков может быть очень сложным.
В опыте, в котором первый шар ударяет второй шар под углом, важно отношение расстояния между шариками D к радиусу шарика R. Если D/R меньше 4, нарушение строя после серии соударений исчезает, поскольку точки соударения постепенно сдвигаются к плоскости, в которой расположены шары, и удары становятся все менее косыми. Если же D/R больше 4, нарушение строя будет нарастать, поскольку точки соударений будут сдвигаться по искривленной поверхности шара дальше от плоскости, в которой расположены шары.
1.43. Падение нескольких мячей
Допустим, мы роняем два мяча примерно с высоты метра, причем вверху располагается бейсбольный, а внизу — баскетбольный мяч (рис. 1.16а). Хотя при падении по отдельности с такой высоты ни один из мячей не отскочит от пола на заметную высоту, при падении пары мячей получается неожиданный результат. Баскетбольный мяч остается лежать неподвижно на полу, а бейсбольный подпрыгивает сильно, иногда даже к потолку (рис. 1.16б). При этом высота, на которую подпрыгнет бейсбольный мяч, всегда больше, чем сумма высот, на которые отскочили бы по отдельности бейсбольный и баскетбольный мячи. (Будьте осторожны. Если удар придется не по центру баскетбольного мяча, бейсбольный мяч может отлететь в сторону, а при такой скорости он может сильно ударить.) Если повторить опыт, но на бейсбольный мяч сверху положить еще один — маленький упругий мяч, тот взлетит как ракета и может подпрыгнуть даже выше, чем бейсбольный мяч, хотя и получит меньше энергии.
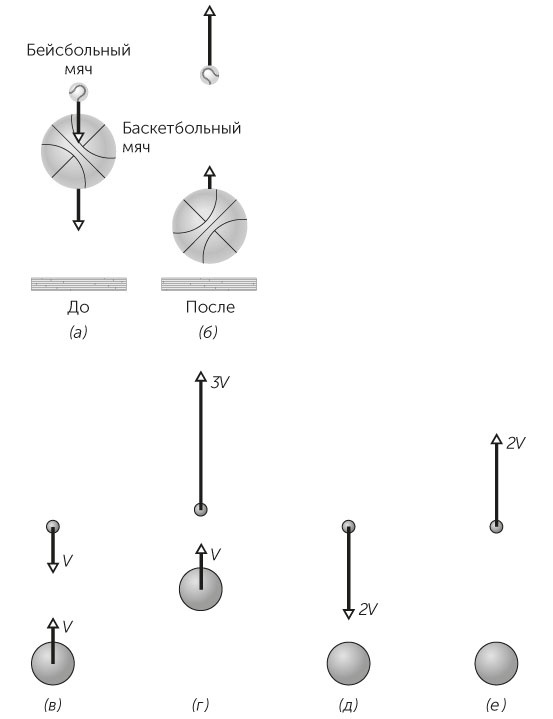
Рис. 1.16 / Задача 1.43. а) До и б) после того, как баскетбольный и бейсбольный мячи вместе брошены на твердый пол. в) До и г) после столкновения очень большого и очень маленького мячей. д) До и е) после столкновения с точки зрения большого мяча.
В теории, если мячи правильно подобраны, верхний мяч из пары брошенных может подпрыгнуть на высоту, в 9 раз большую, чем высота, с которой они были сброшены. С тремя мячами, опять же правильно подобранными и, конечно, при идеальных условиях, верхний мяч может подпрыгнуть на высоту, в 49 раз превышающую высоту, с которой они сброшены. Можно экспериментировать со множеством различных мячей, например с мячиками для пинг-понга, мячами-попрыгунчиками (суперупругие мячики) или теннисными мячами. Как нужно подбирать мячи в группе, чтобы верхний мяч подпрыгнул на большую высоту, и почему он прыгает так высоко?
ОТВЕТ • Когда падает группа из двух мячей, нижний отскакивает от пола, но сталкивается с верхним, который все еще продолжает падать. При соударении энергия передается от нижнего мяча к верхнему, и он приобретает скорость, направленную вверх. Если задаться целью передать максимальную энергию верхнему мячу, нужно, чтобы нижний мяч остановился. Если мячи упругие, наибольшее количество энергии передается, когда масса нижнего мяча в три-четыре раза больше массы верхнего. Примерно такое соотношение у баскетбольного и бейсбольного мячей.
Если же стремиться к тому, чтобы верхний мяч подпрыгнул как можно выше, его нужно выбирать как можно более легким по сравнению с нижним. Высота, на которую подпрыгнет верхний мяч, пропорциональна квадрату скорости, полученной им при столкновении. Если масса верхнего мяча много меньше массы нижнего, верхний мяч получит большую скорость, и сможет подскочить на высоту, в 9 раз большую, чем высота, с которой он падал.
Чтобы понять результат, рассмотрим скорости мячей перед самым столкновением. Верхний мяч падает со скоростью V, а нижний летит вверх с такой же скоростью V (рис. 1.16в). Если соударение абсолютно упругое, верхний мяч приобретет скорость 3V (рис. 1.16 г). Это может показаться неверным, но представьте на мгновение, что вы — первый мяч, и посмотрите на ситуацию с его точки зрения: вы увидите, что верхний мяч приближается к вам со скоростью 2V (рис. 1.16д), упруго отражается от вас и летит прочь со скоростью 2V (рис. 1.16е). А теперь вернитесь к своей собственной точке зрения. Верхний мяч летит прочь от нижнего с относительной скоростью 2V. А что делает нижний мяч? Поскольку масса верхнего мяча мала, соударение сколько-нибудь существенно не изменит скорость тяжелого нижнего мяча, и она по-прежнему будет примерно равна V, так что скорость верхнего мяча будет равна V+2V=3V.
Если рассматривать падение группы мячей, нужно их расположить так, чтобы их массы убывали снизу вверх. Когда нижний мяч отскакивает от пола, он передает часть энергии второму мячу. Как только второй мяч полетит вверх, он ударит летящий вниз третий мяч и передаст часть своей энергии ему. Теперь третий мяч полетит вверх, ударит четвертый мяч и так далее. Если сделать цепочку мячей достаточно большой, теоретически можно верхний мяч запустить на космическую орбиту.
1.44. Короткая история. Разорительный фокус
Когда Джон Макбрайд был студентом в Хьюстоне, он вместе с еще двумя студентами экспериментировал с мячами, отправляя пару мячей — софтбольный и баскетбольный — в свободное падение с высоты третьего этажа (из перехода между двумя общежитиями). Каждый раз при падении баскетбольный мяч застывал на земле, а софтбольный — взмывал высоко над их головами, не меньше чем на 10 м над землей. Фокус имел большой успех, но однажды при очередной попытке соударение мячей произошло не по центру, а под углом, и софтбольный мяч влетел в окно кабинета завхоза, разбив все стекла в комнате. Ремонт обошелся в 250 долларов, но последствия могли бы быть гораздо печальнее, а наказание — более суровым, если бы в комнате в этот момент оказался сам завхоз.
1.45. Карате
Представим себе удар кулаком, при котором сжатый кулак (ладонью вверх) от пояса выносится вперед и потом поворачивается ладонью вниз. Почему при нанесении этого удара учат соблюдать следующие меры предосторожности: подойти к противнику нужно на длину разогнутой руки, но не ближе (каратист не должен при этом наклоняться вперед), а контакт с противником должен происходить в момент, когда кулак прошел 90% пути (чтобы оставшиеся 10% пути кулак прошел в теле противника)? Почему каратист поворачивается в момент начала удара? Почему удар кулаком, рубящий удар, удар ногой и другие удары обычно стараются нанести так, чтобы площадь контакта была минимальной? С какой скоростью и с какой силой профессионалы могут бить кулаком или ногой и какая энергия при этом передается? Почему, когда профессионал ломает противнику кость, его собственная кость при этом не ломается? Зачем, когда каратист раскалывает стопку предметов (например, досок), предметы прокладываются разделителями (например, карандашами)?

