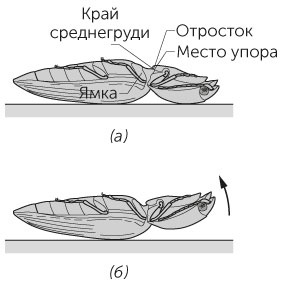
Рис. 1.14 / Задача 1.40. а) Жук-щелкун лежит на спине, отросток уперся в край среднегруди, мышцы напряжены. б) Отросток соскочил с упора и попал в ямку. Жука подбрасывает вверх.
Первоначальное медленное сокращение мышц позволяет жуку накопить энергию. Мгновенное высвобождение этой энергии обеспечивает такой мощный прыжок. Чтобы совершить следующий прыжок, энергию снова нужно накопить, а это требует времени. Подобный метод — накопление энергии и мгновенное ее высвобождение — используют многие виды животных, чтобы совершить быстрое движение, когда нужно либо добыть себе пищу, либо увернуться и самому не стать чьей-то добычей.
Похожий метод применяют и раки-богомолы. Их атакующая вторая пара ногочелюстей согнута и прижата к телу в седловидной выемке. В спокойном состоянии в мышцах выемки происходит медленное накопление энергии, подобно энергии сжатой пружины. Конечность удерживается на месте защелкой, которая отпускается, как только напряжение в мышцах выемки достигает максимума. В это мгновение от нее ногочелюстям передается огромная энергия, и они «выстреливают» в жертву. Пузырьки, о которых шла речь выше и схлопывание которых порождает относительно мощную звуковую волну, возникают из-за уменьшения давления за быстро движущимся в жидкости телом.
1.41. Короткая история. Рекордный вес взят
В тяжелой атлетике разного рода рекорды обновляются довольно часто. Однако самый большой вес, когда-либо поднятый человеком без помощи приспособлений, был взят в 1957 году американским тяжелоатлетом Полом Андерсоном. И этот рекорд не побит до сих пор. Атлет поднял груз методом бэклифта (спиной). Он встал, наклонившись вперед и согнув ноги в коленях. Перед ним стояла низкая скамейка, о которую он опирался руками и от которой мог оттолкнуться. Над ним стояла укрепленная и положенная на прочные стойки деревянная платформа — на ней лежали части автомобиля и сейф, наполненный свинцом. Андерсон плечами смог оторвать от опор груз весом 2845 кг!
Пожалуй, не менее впечатляет рекорд миссис Максвелл Роджерс из города Тампа, установленный в апреле 1960 года. Она увидела, что автомобиль, который ремонтировал ее сын, соскочил с домкрата, стоявшего под бампером, и придавил парня. Она бросилась к автомобилю, приподняла его и держала, пока сосед вытаскивал из-под машины ее сына. Автомобиль весил 1620 кг, из которых она подняла минимум четверть веса, правда, при этом повредила позвоночник. (Свидетельства такого рода периодически появляются в газетах. В момент стресса абсолютно нетренированный человек может поднять вес, который в обычном состоянии, скорее всего, поднять не смог бы.)
1.42. Соударения в цепочке шаров и игрушка «маятник Ньютона»
Если мяч ударяется о неподвижный мяч, при каких условиях второй мяч получит наибольшее количество энергии от первого? А получит ли он наибольшую скорость при тех же условиях? Как изменится ответ, если мяч ударяется в цепочку неподвижных мячей?
Предположим вначале, что движется больший мяч, а покоящийся мяч имеет меньшие размеры. Можно ли увеличить энергию, переданную меньшему мячу, если между этими двумя мячами будут находиться другие мячи? Если да, то какими должны быть массы этих мячей?
Допустим, мяч летит прямо в вашу голову. Если вы хотите смягчить удар, то есть уменьшить энергию, переданную мячом голове, нужно ли вам выставить для защиты руку, чтобы получить удар по голове рукой, а не мячом?
Популярная игрушка — «маятник Ньютона» — состоит из нескольких касающихся друг друга подвешенных на нитках шариков, которые могут раскачиваться как маятники (рис. 1.15а). Шарики сделаны из упругого материала, что означает, что лишь небольшая часть энергии шарика теряется при соударении с другими. Отведем крайний левый шарик назад и отпустим его. Он ударит следующий шарик. Почему после серии соударений отклонится только крайний шарик справа?
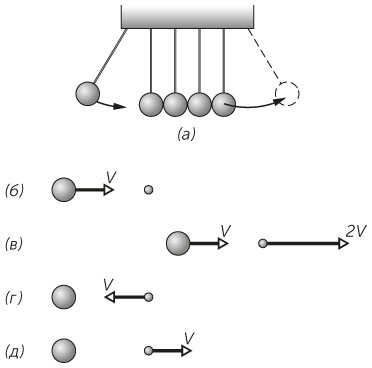
Рис. 1.15 / Задача 1.42. а) Крайний слева шар отпущен, крайний справа отскакивает в сторону. б) До и в) после столкновения очень большого и очень маленького шаров. г) До и д) после столкновения с точки зрения большого шара.
Перевесим шарики так, чтобы между ними было небольшое расстояние, и пошлем первый шарик ко второму под небольшим углом. Хотя первый удар получится косым, по мере того как соударения распространятся по цепочке, нарушение строя шариков постепенно исчезнет. Но если увеличить расстояние между шариками и повторить опыт, нарушение строя будет с каждым ударом возрастать. Удары даже могут вообще прекратиться, если какой-нибудь шар получит совсем косой удар и при раскачке не попадет в следующий шар. Почему при косом ударе крайнего шара со временем, в зависимости от расстояния между шарами, либо произойдет восстановление порядка в строю шаров, либо строй будет разрушаться?
ОТВЕТ • Второй шар получает от первого максимальную энергию, когда его масса равна массе первого шара. Если оба шара идеально упругие, почти вся энергия при столкновении переходит ко второму шару, а значит, его скорость будет такой же, какой была до соударения у первого шара, а тот, следовательно, остановится.
Второй шар приобретет максимальную скорость в том случае, когда его масса много меньше массы первого шара. Пусть V — скорость первого шара (рис. 1.15б). Если отношение масс очень велико и соударение абсолютно упругое, второй шар может приобрести скорость 2V (рис. 1.15в). Это может показаться неправильным, но на секунду попробуем посмотреть на происходящее с точки зрения первого шара. Нам кажется, что второй шар движется на нас со скоростью V (рис. 1.15 г), упруго отскакивает и улетает со скоростью V (рис. 1.15д). Теперь вернемся в нашу обычную систему отсчета. Второй шар улетает от первого с относительной скоростью V. А что делает первый шар? Поскольку второй шар имеет такую маленькую массу, соударение не сильно влияет на скорость первого шара. И она по-прежнему останется равной V. Таким образом, скорость второго шара должна быть равна V + V = 2V. Если происходит цепная реакция таких соударений, то скорость, сообщенная каждым столкновением, примерно удваивается по сравнению с предыдущим столкновением.
Если массы крайних шаров заданы и мы хотим передать максимальную энергию меньшему шару, нужно так выбрать массу каждого промежуточного шара, чтобы она была равна среднему геометрическому масс шаров, находящихся по разные стороны от него. (Среднее геометрическое двух масс — это корень квадратный из произведения этих масс.) При другом выборе масс промежуточных шаров тоже можно получить выигрыш в передаваемой энергии, но не такой большой.
Этот вывод применим и к удару мячом по голове. Если подставить руку на пути летящего мяча, это только увеличит передаваемую энергию, поскольку рука как раз имеет массу, среднюю между массами головы и мяча. И все же подставить руку стоит, поскольку она шире мяча и сила удара по голове распределится на большую площадь.

