Итак, мы избавились от более чем половины ячеек. Посмотрим, что осталось.
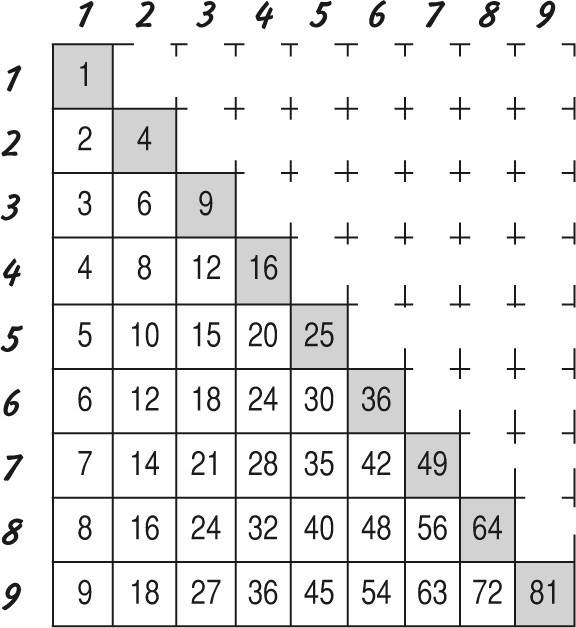
Числа в серых ячейках называются квадратами целых чисел, или просто квадратами. Это результаты умножения каждого числа на само себя. Например, вдоль каждой стороны шахматной доски 8 клеток, поэтому полное количество клеток на доске будет равняться восьми в квадрате. Записывают это так: 82, что соответствует 8 × 8 = 64.

Если вы ненавидите зубрить таблицу умножения, можете заполнить ее ячейки еще одним способом. Сначала можно просто складывать нечетные числа 1, 3, 5, 7 и т. д. Начинаем с 1 + 3 = 4. Затем прибавляем 5, получаем 9, затем 7, получаем 16… Так вы вычислите квадраты всех чисел.
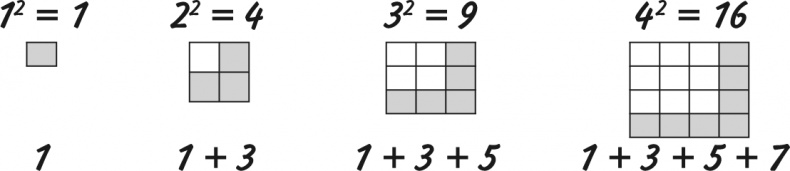
Если взять любую ячейку с квадратом числа и вычитать из нее нечетные числа, начиная с 1, то получатся значения по диагонали, идущей в другую сторону от исходной ячейки.
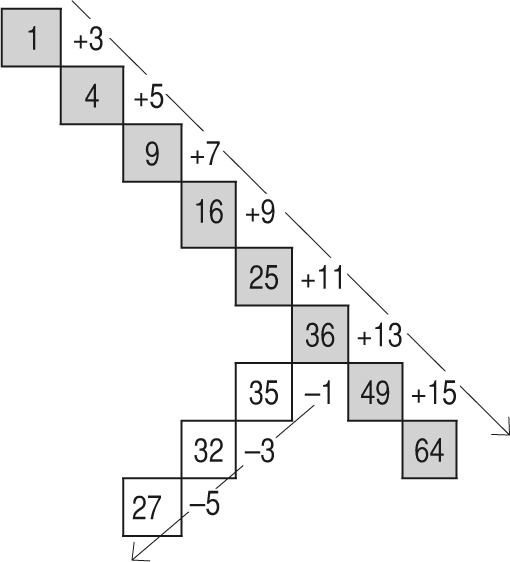
Таким образом, начав с 36 и отняв 1, получим 35, отняв 3, получим 32, вычтя 5, получим 27.
(Сравнив эту диаграмму с таблицей умножения, вы убедитесь, что все совпадает.)
Аналогичным способом, но с помощью четных чисел (2, 4, 6, 8…) можно заполнить и остальные ячейки. Посмотрите на диагональ, идущую ниже диагонали квадратов, ту, где стоят числа 2, 6, 12, 20… Эти значения можно получить, начав с 2, затем прибавив 4, затем 6, потом 8 и т. д. А взяв любое из этих чисел (например, 20), можно найти значения вдоль идущей в другую сторону диагонали – вычитая 2, затем 4, потом 6 (например, 20 − 2 = 18, 18 − 4 = 14 и 14 − 6 = 8).
Такие последовательности нечетных и четных чисел позволяют вывести всю таблицу умножения, ни разу при этом не выполнив умножения как такового!
Фокус с тремя числами
Возьмите три любых последовательных числа: при перемножении первого и последнего всегда получится значение на единицу меньше, чем квадрат числа посередине.
Взяв числа 6, 7, 8 и сверившись с таблицей умножения, мы убедимся, что 6 × 8 = 48, а 7 × 7 (или 72) = 49.
Так будет с любыми последовательно идущими числами. Если известно, что 1482 = 21 904, можете быть уверены, что 147 × 149 = 21 903.
(Почему так происходит? Это одна из тех маленьких загадок, которые мы научимся решать когда перейдем к разделу «Алгебра».)
Простые числа
Простое число делится только на само себя и единицу. Например, число 10 не является простым (оно делится на 1, 2, 5 и 10), число 12 тоже (делится на 1, 2, 3, 4, 6, 12), а вот число 11 – простое (делится только само на себя и на 1). Если попробовать упаковать числа в ящики, не оставляя пустых мест, с простыми числами возникнут сложности, поскольку разделить их на равные части не получится.
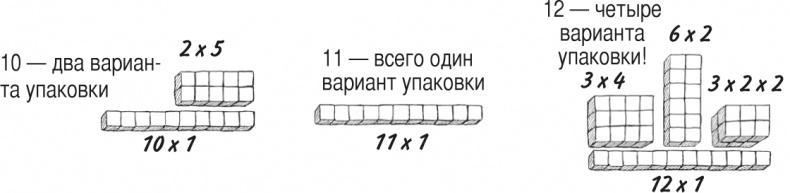
Наименьшее простое число – это 2. Также это единственное четное простое число, поскольку все остальные четные числа делятся на 2. Следующие простые числа: 3, 5, 7, 11, 13, 17, 19, 23… и так далее до бесконечности.
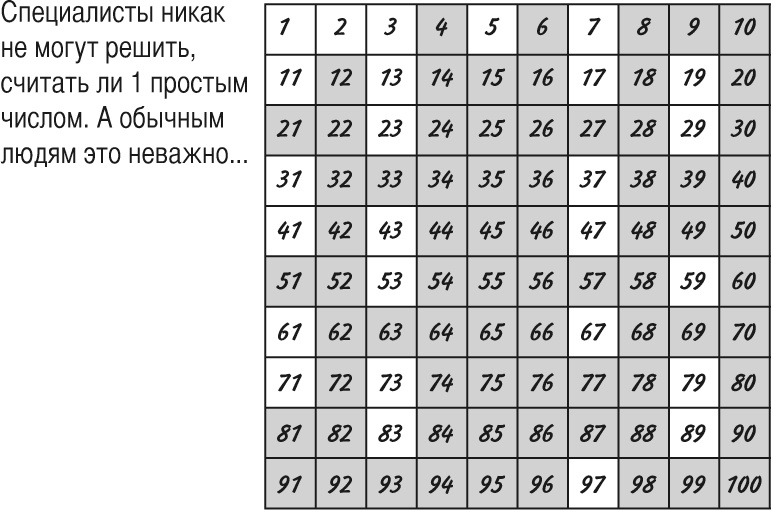
Здесь представлены все числа от 1 до 100, причем числа в белых квадратиках – простые. Легко понять, где простое число наверняка не встретится: со второй строки и ниже простые числа не могут заканчиваться на 2, 4, 6, 8 или 0 (тогда они делились бы на 2) и на 5 (тогда они делились бы на 5). Что никому до сих пор не удалось выяснить, так это где обязательно должно появиться простое число. Был момент всеобщей радости из‑за числа 31, так как поскольку оно простое, простыми также являются 331, 3331, 33 331, 333 331 и т. д. Казалось, любая последовательность троек с единицей в конце даст простое число, и так считали до тех пор, пока кто-то не обнаружил, что 19 607 843 × 17 = 333 333 331. Кстати, если вам удастся найти между простыми числами общую закономерность, ваше имя будут помнить еще долго после того, как имена всех знаменитостей, которыми переполнена сейчас земля, канут в Лету.
Умножение на пальцах
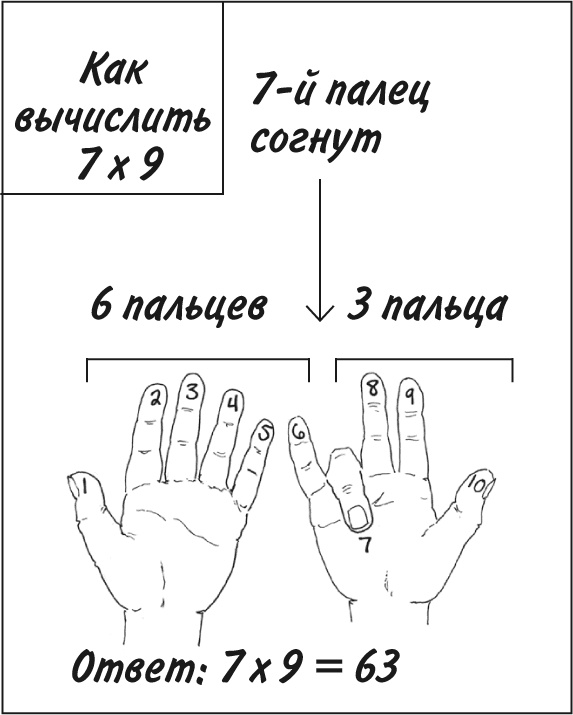
Таблица умножения для числа 9 – одна из самых сложных, но в наши дни почти каждому школьнику знаком изящный способ запоминания.
Поднимите ладони перед собой и представьте, что пальцы пронумерованы от 1 до 10 слева направо. Согните палец, соответствующий числу, которое вы хотите умножить на 9. Посчитайте, сколько пальцев находится слева и справа от согнутого пальца. Это и будет ответ (см. рисунок).
Но есть трюки и похитрее…
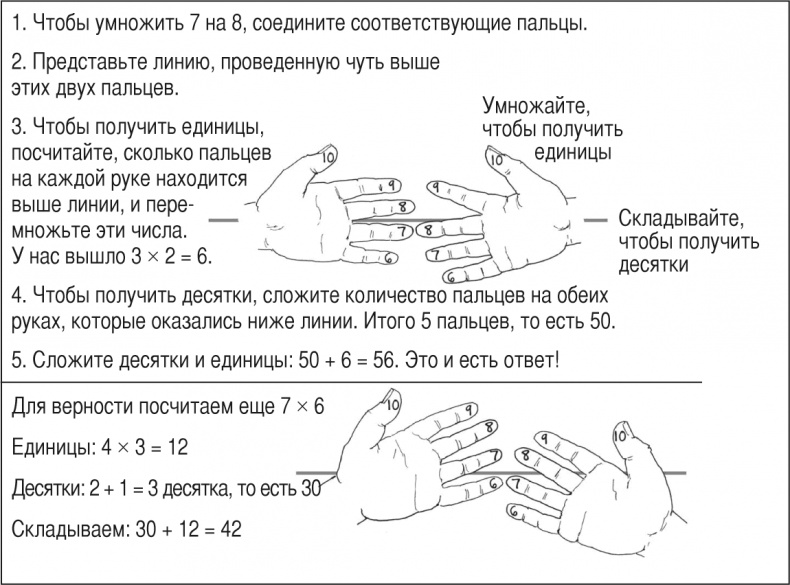
Зная таблицу умножения вплоть до 5 × 5, вы можете посчитать на пальцах любое произведение от 6 × 6 до 10 × 10. Сперва представьте, что пальцы каждой руки пронумерованы как 6, 7, 8, 9, 10.
Умножение больших чисел
Вы проехали 693 мили, чтобы устроить палаточный лагерь где-то у черта на куличках, и по возвращении домой обнаружили, что нет ключей от входной двери, которые вы, скорее всего, выронили, когда разбирали тент. Съездив за ними обратно, вы в итоге проехали по одной и той же дороге четыре раза. Сколько всего миль вы преодолели?
Честно говоря, после таких приключений вряд ли кому-то захочется садиться за подсчеты, но если вы все же решитесь, окажется, что числа выходят далеко за пределы таблицы умножения. Хитрость в том, чтобы умножать небольшими частями, к тому же (о радость!) вам ничего не придется умножать больше чем на 9. Рассмотрим по пунктам, как умножить 693 на 4.

