Возьмем весьма простое выражение:
Иначе его можно записать как 103 × 102 = 105 – это абсолютно то же самое, однако вместо того, чтобы перемножать большие числа, мы просто сложили степени: 3 + 2 = 5. Джон Непер понял, что любое число можно представить в виде степени числа 10, после чего для умножения или деления чисел достаточно лишь складывать или вычитать их степени.
Но вот незадача: такие степени редко бывают красивыми ровными числами, например 78 = 101,89209. Когда степени становятся затейливыми десятичными дробями, их называют логарифмами. Поскольку 78 = 101,89209, можно сказать, что логарифм от 78 равен 1,89209.
Перевод чисел в логарифмы – крайне утомительный процесс, но соратник Непера по имени Генри Бригс облечил его, разработав для подобных преобразований так называемые логарифмические таблицы. Некоторые из таблиц позволяли получить лишь три знака после запятой: 78 = 101,892. А по наиболее точным таблицам Бригса выходило, что 78 = 101,89209460269048. Соответственно, чем точнее логарифмы, тем точнее результат вычислений. (Исаак Ньютон, изучая движения звезд и планет, дошел в вычислении логарифма до 50 знаков после запятой, но его увлеченность граничила с манией.)
Что ж, опробуем логарифмы в деле.

Точный ответ = 1 198 366 848. Погрешность при вычислении с помощью логарифмов составила примерно 1 миллионную!
Быстрый способ вычисления корней
Вы можете находить квадратные и кубические корни путем деления логарифма на 2 и 3.
Будь вы Исааком Ньютоном, которому нужно узнать кубический корень из 591, вы бы сначала нашли по логарифмическим таблицам, что 591 = 102,771587. Затем посчитали бы 2,771587 ÷ 3 = 0,923862. И наконец, переведя 100,923862 в обычное число, получили бы ответ: 8,391942. (Если перемножить 8,391942 × 8,391942 × 8,391942, действительно получится 591.)
Мало того что этот ответ точен – логарифмы позволили сэкономить часы, которые бы ушли на мозгодробительные вычисления!
Глоссарий
Существует много слов для обозначения разных математических понятий, однако эта книга и так достаточно информативна. Поэтому я старался, насколько возможно, обходиться без научной терминологии. Однако все же предоставляю краткий справочник по основным математическим терминам.
E – на экране калькулятора обозначает «экспоненциальную запись», когда результат умножается на степень числа 10.
e – особенное число, равное 2,71828183. Применяется при вычислении прироста чего-либо, например урожая. Также используется при расчете банковских процентных ставок.
Градус – единица измерения углов, обозначается символом °. Также в градусах (Кельвина, Цельсия и Фаренгейта) измеряют температуру.
Делимое – при делении это число, которое делят. В выражении 35 ÷ 5 = 7 число 35 является делимым.
Делитель – при делении это число, на которое делят. В выражении 48 ÷ 4 = 12 число 4 является делителем.
Десятичные дроби – числа с десятичной запятой, такие как 0,667 или 365,26.
Диаметр – линия, соединяющая две точки окружности и проходящая через ее центр.
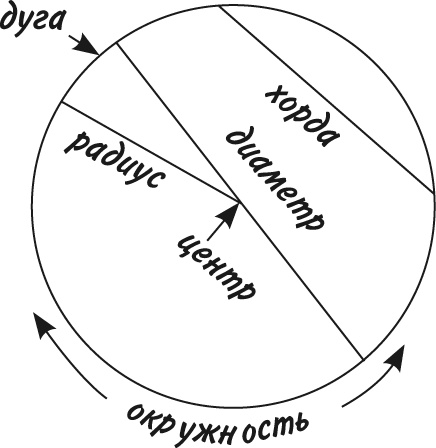
Дуга – участок окружности. Может быть разной величины, от маленького кусочка до почти полной окружности.
Знаменатель – нижнее число в простой дроби. Например, в дроби 4/7 число 7 – это знаменатель.
Иррациональное число – десятичная дробь с бесконечным количеством знаков после запятой, которые не повторяются предсказуемым образом.
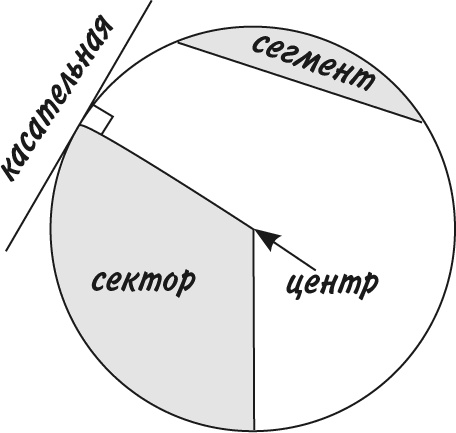
Касательная – прямая линия, которая соприкасается с окружностью в одной точке. Если провести к этой точке радиус, он составит с касательной угол в 90°.
Квадрат и квадратный корень. Возведение в квадрат – это умножение числа на само себя, например 7 × 7 = 49. Действие, обратное этому, называется извлечением квадратного корня, например квадратный корень из 49 равен 7.
Квадратное уравнение – алгебраическое уравнение, в которое входит неизвестное значение в квадрате, например x². Обычно у квадратного уравнения есть два разных решения.
Коэффициент – число, на которое умножается другое число (или содержимое скобок). Например, в выражении 3(2x + 7) число 3 – коэффициент при выражении в скобках, а 2 – коэффициент при x.
Медиана – при наличии упорядоченного набора значений медианой будет значение, стоящее посередине совокупности значений.
Множители – целые числа, на которые заданное число делится без остатка. Множители числа 60: 1, 2, 3, 4, 5, 6, 10, 12, 15, 20 и 30. Простые множители – простые числа, которые нужно перемножить, чтобы получить исходное составное число. Простые множители числа 60: 2 × 2 × 3 × 5 = 60.
Мода – при наличии набора значений модой будет то значение, которое встречается в этом наборе чаще всего.
Неравносторонний треугольник – треугольник, у которого все стороны разной длины.
Нечестный официант (см. подраздел «Загадка про нечестного официанта») – забудьте о 30 фунтах! В итоге женщины заплатили 27 фунтов, 25 из которых попали в кассу, а 2 остались у официанта.
Ноль – пожалуй, самое сложное из чисел, ведь некоторые люди даже не уверены, что оно является числом. Если считать его числом, оно порождает множество проблем, особенно при попытке на него делить. А если это не число, то как оно может получиться из других чисел, например 2 − 2 = 0?
Округление – замена неудобного числа более простым числом, близким к нему по значению.
Окружность – замкнутая линия, граница круга.
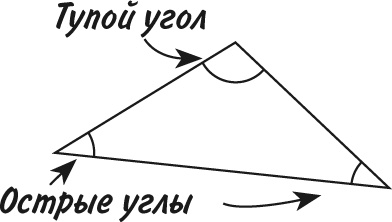
Острый угол – угол, величина которого меньше 90° (то есть меньше прямого угла).