При расчете площади или объема всегда используйте одинаковые единицы измерения. У нас радиус в миллиметрах, а высота в метрах, так что будем считать все в метрах, чтобы в итоге получить кубические метры. Преобразуем радиус: 80 мм = 0,08 м. Теперь подставим r = 0,08 и h = 0,3 в формулу:
объем банки = π × (0,08)² × 0,3 = π × 0,0064 × 0,3 = 0,00603 м³
Заглянув в табличку в подразделе «Метры, литры и граммы», мы видим, что в 1 кубическом метре 1000 литров. Стало быть, наша таинственная банка вмещает 0,00603 × 1000 = 6,03 л.
Прежде мы выяснили, что нам нужно 6 банок краски объемом 750 мл для стен и еще 2 банки для потолка – всего 8 банок. Сколько это в литрах? 750 мл = 0,75 л, значит, в 8 банках 8 × 0,75 = 6 л. Отлично, одной огромной банки как раз хватит на все стены и потолок!
Быстрый способ
Если у вас есть рулетка, вы можете рассчитать объем цилиндра, не связываясь с числом π. Для этого нужно измерить его окружность с, диаметр d и высоту h. Длина окружности неявно вводит π в расчеты, и получается изумительно простая формула:
объем цилиндра = dch/4
Сфера
Около 2250 лет тому назад греческий ученый и математик Архимед совершил множество потрясающих открытий. Но лишь одно изображено на его могильной плите: Архимед был первым, кто доказал, что сфера, вписанная в цилиндр, занимает ровно 2/3 его объема. Иначе говоря, если взять банку с бобами в точности такого размера, чтобы в нее входил теннисный мяч, этот мяч вытолкнет наружу ровно 2/3 бобов. Благодаря Архимеду у нас теперь есть формула объема сферы.
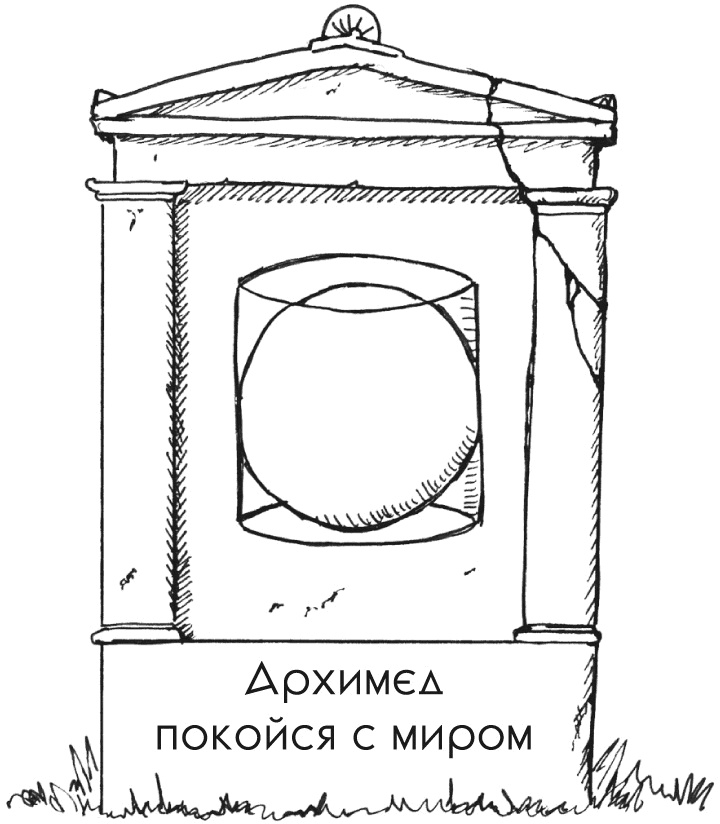
Итак, возьмем сферу и обозначим ее радиус r.
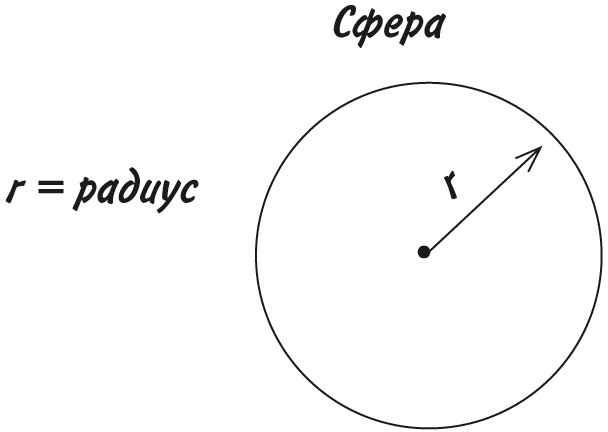
Сначала выведем формулу объема наименьшего цилиндра, в который помещается эта сфера. Возьмем обычную формулу объема цилиндра πr²h, однако учитывая, что высота цилиндра в нашем случае равна 2r, объем наименьшего цилиндра будет πr² × 2r = 2πr³.
Согласно Архимеду, сфера занимает 2/3 этого объема, следовательно, объем сферы = 2/3 × 2πr³. В итоге получается:
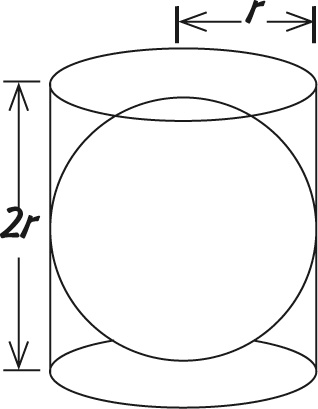
Раз уж мы занялись сферой, стоит упомянуть, что если разрезать ее пополам, площадь круга на срезе будет равна πr². А площадь поверхности сферы вчетверо больше площади круга, поэтому
площадь поверхности сферы = 4πr²
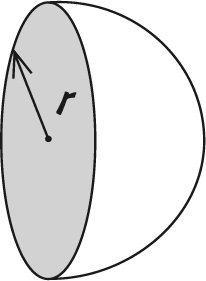
Формула объема сферы – еще одна весьма популярная на уроках геометрии тема, совершенно бесполезная в обыденной жизни: скажите на милость, как измерить радиус чего-то вроде футбольного мяча относительно его центра? Гораздо проще измерить его окружность с и воспользоваться такой формулой:
Если вы ученый-ракетостроитель и вам нужен более точный результат, то вычисляйте так:
объем сферы = с³/59,2176264
Однако если вы ракетостроитель и учите математику по этой книге, то у нас у всех серьезные проблемы, не так ли?
Пифагор и его теорема
Пифагор жил примерно за 300 лет до Архимеда и прославился в первую очередь своей знаменитой теоремой: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов его катетов.
Звучит несколько замысловато, но взгляните на рисунок, и вы все поймете. Если взять прямоугольный треугольник и пририсовать к каждой его стороне квадрат, то площади двух меньших квадратов в сумме будут равны площади большого квадрата.
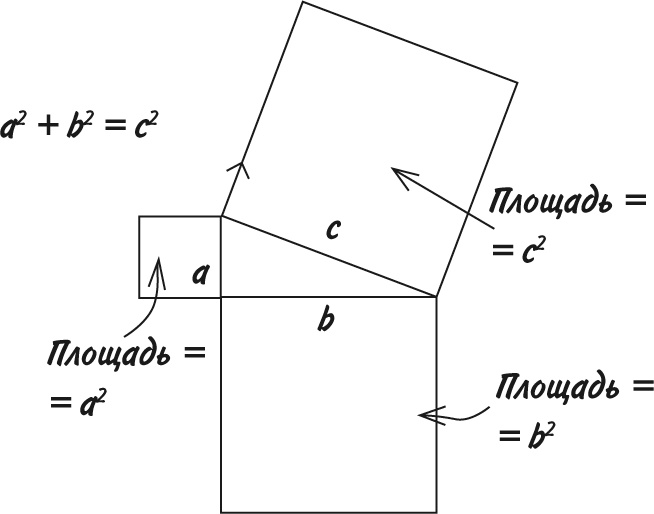
Если вас беспокоит вопрос, зачем кому-то понадобилось лепить к сторонам треугольника квадраты, не волнуйтесь, польза теоремы не в этом. Лучше представьте, что вы по диагонали пересекаете футбольное поле. Если размер поля 100 м × 70 м, какое расстояние вам нужно преодолеть?

Вычисления будут не совсем простыми, поэтому, получив ответ, стоит убедиться, что он правдоподобен! По рисунку видно, что результат должен быть больше 100 м, но меньше 170 м.
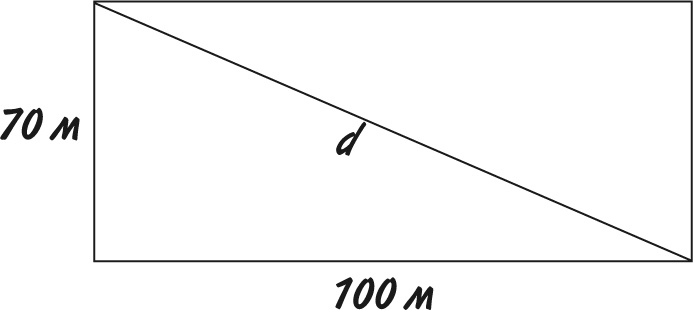
Обозначим диагональ буквой d.
Согласно теореме Пифагора, d² = 100² + 70²
Вычисляем: d² = 10 000 + 4900 = 14 900
Теперь нужно извлечь квадратный корень из 14 900. Иными словами, при умножении какого числа на само себя получится 14 900?
Если у вас нет калькулятора, самый простой способ извлечения корней – догадка и корректировка. Положим, вам кажется, что ответ может равняться 120, тогда считаем: 120 × 120 = 14 400. Довольно близко, но все же меньше, чем надо. Ладно, попробуем 123 × 123 = 15 129. Выходит больше, чем 14 900. Проверим еще один вариант 122 × 122 = 14 884. Уже совсем рядышком, однако теперь все же посчитаем на калькуляторе.

Введите ‹14900 √› и получите 122,065.

