У этой пары есть 10 минут, чтобы добраться до родильного дома, а велосипедист едет со скоростью 20 миль в час. Успеют ли эти бедолаги? Нам надо выяснить, за какое время можно преодолеть 3 мили, двигаясь со скоростью 20 миль в час. Используя формулу t = d/s, получим: t = d/s = 3/20.
Поскольку скорость выражена в милях в час, в результате выйдет 3/20 часа, однако нам нужно время в минутах. В часе 60 минут, стало быть, в минутах это будет 3/20 × 60 = 9 минут. Так что, когда парочка доберется до роддома, в запасе у них останется всего минута. Будем надеяться, что в приемной нет очереди.
Комбинирование разных скоростей
Допустим, вы должны преодолеть на машине 400 миль максимум за 8 часов. Если всю дорогу ехать с постоянной скоростью, формула s = d/t подскажет, что она должна равняться 400 ÷ 8 = 50 миль в час.
Теперь предположим, что вы проехали первые 200 миль со скоростью 40 миль в час. С какой скоростью нужно ехать оставшиеся 200 миль, чтобы уложиться в отведенные 8 часов? Может показаться, что подходящий ответ – 60 миль в час, но это неверно!
Сначала выясним, сколько еще осталось времени. Раз вы проехали 200 миль со скоростью 40 миль в час, воспользуемся формулой t = d/s, чтобы узнать, сколько вы уже находитесь в пути: 200 ÷ 40 = 5 часов. Значит, оставшиеся 200 миль нужно преодолеть за 3 часа, поэтому ехать надо со скоростью 200 ÷ 3 = 66,7 миль в час.
Проценты
С процентами мы сталкиваемся повсюду – от магазинов до банков, от платежных ведомостей до результатов экзаменов. Несложные проценты, такие как 50 %, 33 % или 25 %, часто используются для описания специальных предложений в торговых точках, однако если вы имеете дело с налогами или кредитной картой, вам знакомы куда более замысловатые процентные соотношения. Так или иначе, проценты стоят того, чтобы в них разобраться. Как обычно в математике, изначально все исключительно просто: один процент обозначается как 1 %, и это в точности соответствует 1/100, или 0,01. А сто процентов, или 100 %, – это то же самое, что 100/100, то есть 1.
От дробей к процентам
Чтобы преобразовать простую дробь в проценты, нужно разделить верхнюю часть дроби (числитель) на нижнюю часть (знаменатель) и умножить на 100. Вот как перевести в проценты дробь 2/5.
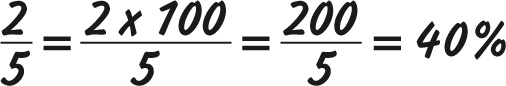
Также проценты можно преобразовать обратно в дробь, разделив их на 100. Переведем 40 % в простую дробь:
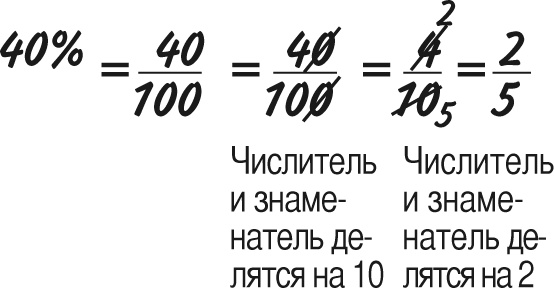
Проценты и десятичные дроби тесно взаимосвязаны, поскольку проценты – это первые две цифры после запятой в десятичной дроби: например 0,85 = 85 %. Когда после запятой стоит ноль, его важно учитывать! 0,03 = 03 %, или просто 3 %. Если же после запятой много чисел, следует передвинуть запятую на два знака. Допустим, вы хотите определить, сколько в процентах будет 1/16: вводим в калькулятор 1 ÷ 16 и получаем 0,0625, что соответствует 6,25 %.
Уклон дороги
Поднимаясь на велосипеде в гору, вы можете встретить дорожный знак, где обозначен уклон дороги в процентах – чем круче подъем, тем это значение больше. Вот как оно вычисляется:
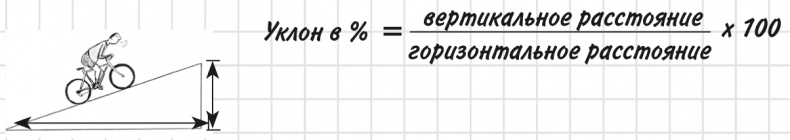
Вертикальное расстояние, на которое вы поднимаетесь вверх, делится на горизонтальное расстояние, на которое вы продвигаетесь вперед. Например, на каждые 4 метра движения вперед вы поднимаетесь на 1 метр. В прежние времена сказали бы, что это уклон 1 к 4, а нынче записывают как дробь 1/4 и переводят в проценты. Следовательно, уклон 1 к 4 будет обозначен на дорожном знаке как 25 %. На первый взгляд это немного, однако если вы не в идеальной физической форме, придется слезть с велосипеда и катить его рядом.
Большинство простых дробей невозможно точно преобразовать в проценты (как и в десятичные дроби). Ниже приведены самые распространенные значения в процентах и соответствующие им дроби; звездочками помечены округленные значения.
50 % = 1/2
25 % = 1/4
75 % = 3/4
33 %* = 1/3
67 %* = 2/3
10 % = 1/10
20 % = 1/5
40 % = 2/5
60 % = 3/5
17 %* = 1/6
12,5 % = 1/8
Деньги и проценты
Большинство денежных единиц четко соотносятся с десятичными дробями и процентами. Например, в британском фунте 100 пенсов, в одном евро 100 евроцентов, в долларе США тоже 100 центов. Это существенно упрощает расчеты, связанные с деньгами.
Если разделить 29 фунтов между двумя людьми, каждому человеку достанется 14½ фунта, или 14,5 фунта (поскольку 1/2 = 0,5). Это значение выглядит несколько странно, поэтому представим его с двумя знаками после запятой. То есть каждому достанется 14,50 фунта, или 14 фунтов и 50 пенсов.
Так как 100 % = 1, а 100 пенсов = 1 фунт, 1 % от фунта – это 1 пенс. Если в кофейне Barstucks чашка кофе и пирожное стоят 7 фунтов плюс 15 % сервисного сбора, несложно посчитать, сколько это будет: 15 % от 1 фунта = 15 пенсов, следовательно, 15 % от 7 фунтов – это 15 × 7 = 105 пенсов. Значит, всего нужно заплатить 7 + 1,05 = 8,05 фунта, и не пытайтесь всучить им 8 фунтов – как знать, что они добавят во взбитые сливки, когда вы придете в следующий раз.
Как выгадать на скидках
Умение сравнивать дроби и проценты поможет вам сэкономить. Предположим, вам нужно купить много батареек, и вы нашли три магазина, предлагающих разные скидки:
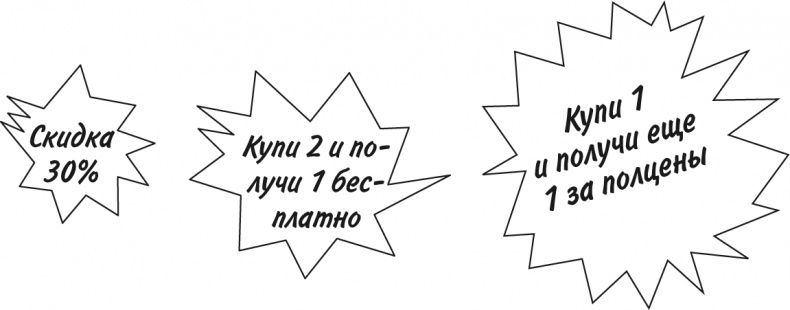
Без учета скидок батарейки в этих магазинах стоят 50 пенсов – где же их выгоднее купить? Для этого необходимо выяснить акционную цену одной батарейки.

