4,40 фунта за чашку кофе? Неудивительно, что Малькольм был в шоке!
Что можно и чего нельзя
В алгебре есть еще несколько на первый взгляд странных правил, поэтому, чтобы они стали понятнее, представим себе множество одинаковых коробков спичек. В каждом содержится m спичек, так что если мы отложим в сторону три коробка, общее количество спичек в них составит 3 × m, или просто 3m. Число 3 здесь – коэффициент при m.

Теперь, разобравшись с коробками, перейдем к правилам и выясним, как их применять к нашим спичкам.
1. Коэффициент можно умножать на число
Если добавить еще одну стопку из трех коробков…

… то 2 стопки по 3m в сумме дадут 6m.
2. Прибавлять число к коэффициенту нельзя
Если вы где-то нашли три спички…
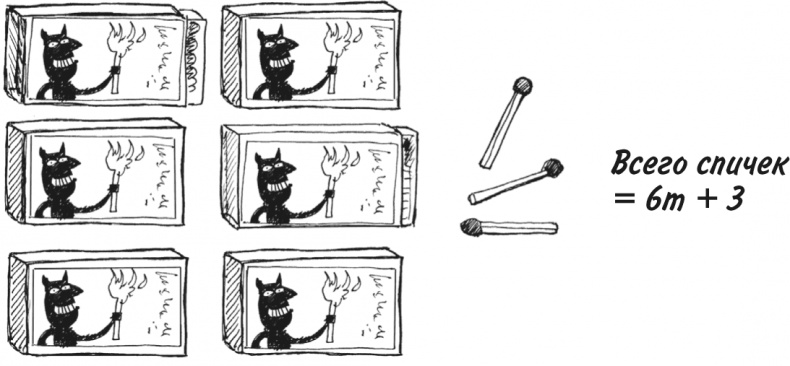
Видите, теперь у нас 6m + 3 спички. Нельзя прибавлять 3 к 6, чтобы получить 9m!
3. Коэффициенты можно складывать, если при них одна и та же буква
Если взять еще два коробка…
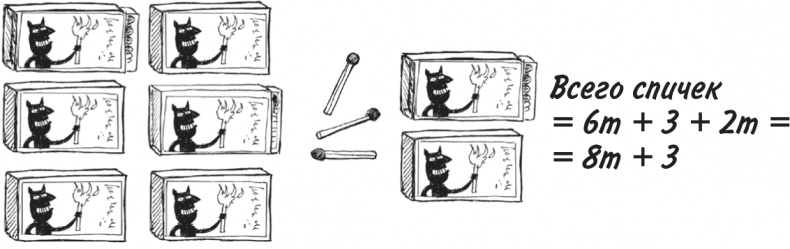
Как видите, складывать 6m и 2m, чтобы получить 8m, можно, но 3 прибавить к 8m по-прежнему нельзя.
Вот еще три правила. Не волнуйтесь, если сейчас они покажутся вам непонятными, чуть позже мы их применим, и все прояснится.
4. Когда знак «минус» стоит перед скобками, избавляясь от них, надо поменять все знаки внутри скобок на противоположные
В выражении вроде 3 − (2x − 4) все, что внутри скобок, следует умножить на –1. Избавившись от скобок, вы получите 3 − 2x + 4. Вместо +2х стало −2х, а вместо −4 стало +4.
5. Если умножить букву на саму себя, получается буква в квадрате
Таким образом, y × y превратится в y² (что такое числа в квадрате, мы обсуждали в разделе «Квадраты и квадратные корни»), а 4y × 3y – в 12y². Коэффициенты перемножаются, а у буквы появляется знак квадрата.
6. При перемножении разных чисел и букв числа умножаются, а буквы пишутся вместе
Поэтому 2x × 4y = 8xy. Такие ситуации часто возникают при умножении содержимого скобок, например: 3p(7q − 2p) = 21pq − 6p².
Итак, давайте посмотрим, как это все может нам пригодиться.
Разгадка тайн математики с помощью алгебры
Алгебра бывает крайне полезна при решении задач и головоломок. Вот вам кое-что для начала.
Земельная афера
Бэтчап Билдингз решил приобрести надел земли у фермера Шарпа. Обе стороны сошлись на том, что это должен быть квадратный участок 20 м × 20 м, то есть площадью 400 квадратных метров, или м². Однако приехав осмотреть землю, Бэтчап увидел, что участок имеет прямоугольную, а не квадратную форму!

Честно ли поступает фермер?
Хотя мы не знаем, на сколько метров стороны участка длиннее или короче, нам известно, что это одна и та же величина, давайте назовем ее x. Нарисуем схему участка.
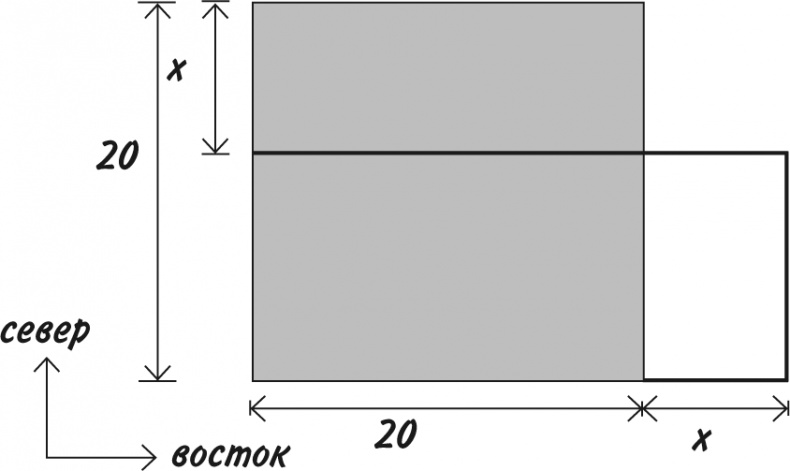
Серым цветом показано, как бы выглядел участок, будь это квадрат 20 м × 20 м. Размеры же прямоугольника: (20 − x) в северном направлении и (20 + x) в восточном. Чтобы узнать его площадь, перемножим эти значения и получим (20 − x) × (20 + x); знак умножения обычно не пишется: (20 − x)(20 + x).
 При перемножении двух выражений в скобках все, что находится внутри одной пары скобок, умножается на все, что находится внутри другой пары.
При перемножении двух выражений в скобках все, что находится внутри одной пары скобок, умножается на все, что находится внутри другой пары.
Для этого раскрываем первые скобки и умножаем каждый элемент в них на вторые скобки. Получаем:
(20 − x)(20 + x) = 20(20 + x) − x(20 + x) =
= 400 + 20x − 20x − x² =
= 400 − x²
Как видите, раскрывая −x(20 + x), мы первым делом умножаем −x × 20 = −20x. Обратите внимание, знак «минус» никуда не исчезает. И наконец, умножаем −x × x, что дает −x². В следующей строке +20x и −20x взаимоуничтожаются, и мы получаем любопытный результат: 400 − x². О чем это говорит?
Будь участок квадратным, Бэтчап приобрел бы обещанные 400 квадратных метров земли. Однако после изменения формы участка его площадь уменьшилась на x². И чем больше значение x, тем больше земли теряет Бэтчап. (Помните, буква x обозначает, насколько стороны длиннее/короче одна другой.)
Если участок на 5 метров длиннее в одном направлении и на 5 метров короче в другом, тогда x = 5. Мы можем вычислить площадь такого участка двумя способами. Во-первых, взяв полученный ранее ответ 400 − x² и подставив вместо x число 5. Площадь составит 400 − 52, то есть 400 − 25 = 375. Во-вторых, просто перемножив длины сторон прямоугольника. В северном направлении это 20 − 5 = 15, а в восточном – 20 + 5 = 25. Тогда площадь равна 15 × 25 = 375. Оба ответа совпадают, стало быть, алгебра работает как надо!

