Перед отрицательными числами обязательно нужно ставить знак «–». Перед положительными числами тоже положено ставить знак «+», но делать мы это будем не всегда.
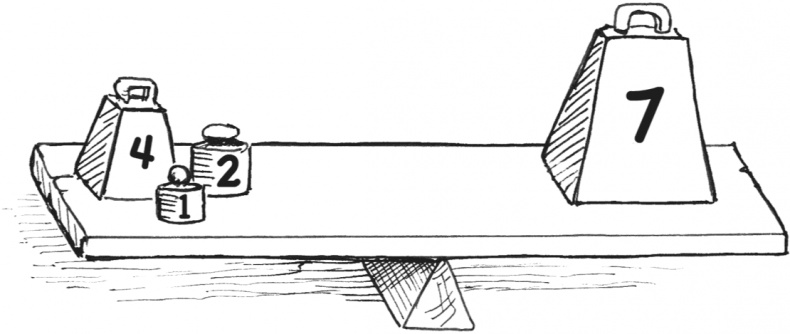
Уравнение можно представить себе в виде доски-качалки, где знак «равно» – точка опоры. Положительные числа – это грузы, прижимающие доску к земле, а отрицательные – воздушные шары, тянущие ее вверх.
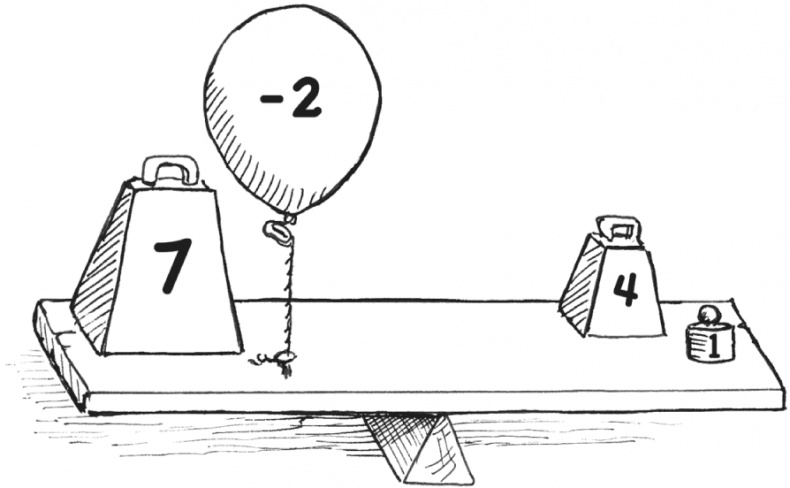
Если хотите переместить числа с места на место на одном конце доски, их знаки нужно перемещать вместе с ними. Поменяв местами числа с левой стороны, получим:
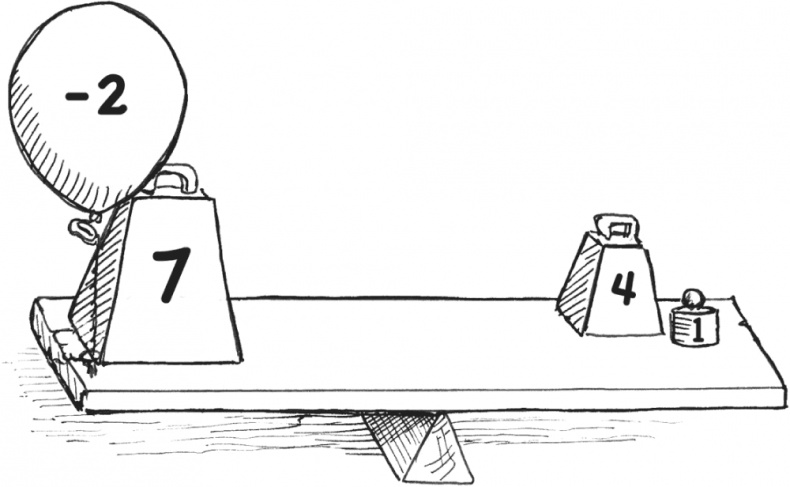
Знак «минус» должен оставаться перед числом 2, иначе уравнение станет неверным. Перед 7 появился знак «плюс» как напоминание, что оно положительное. Предположим, что нам нужно оставить в левой части уравнения только число +7. Существует всего одно золотое правило.
С уравнением можно делать все что угодно
[8] при условии, что с его обеими частями производятся одни и те же действия.
Чтобы в левой части осталось только +7, нужно избавиться от –2. Для этого добавим +2; однако, согласно правилу, это число нужно добавить к обеим частям уравнения.
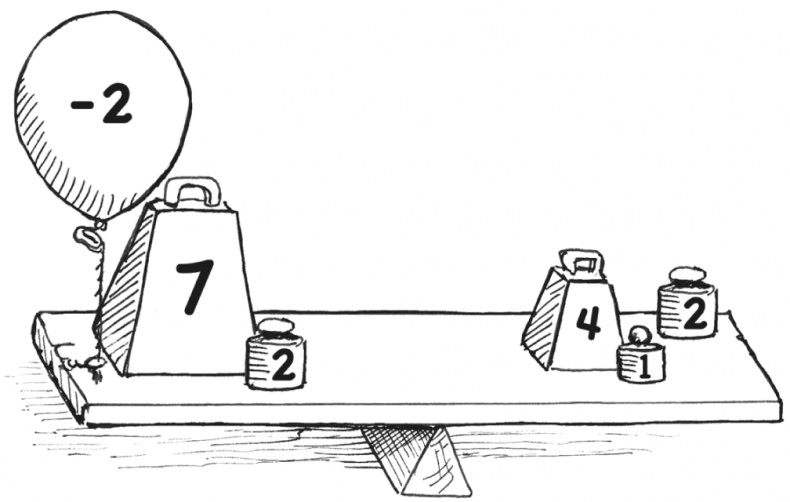
−2 и +2 с левой стороны уравнения взаимоуничтожатся, то есть дадут 0. С правой же стороны +2 останется, и мы получим:
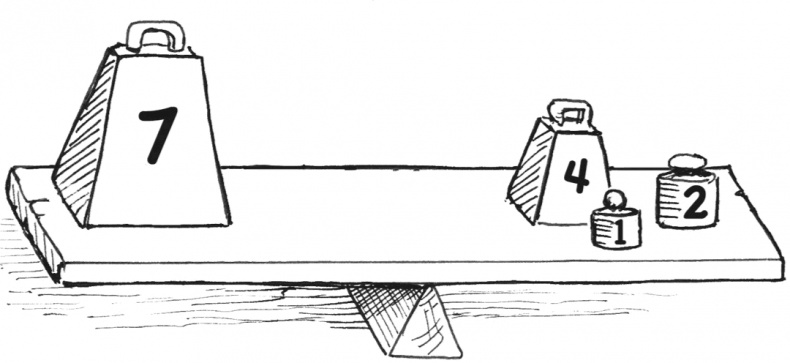
Выполнив подсчеты, вы убедитесь, что 7 и вправду равняется 4 + 1 + 2. При этом мы продемонстрировали маленькую хитрость.
При переносе числа через знак равенства меняется его знак! То есть «−» меняется на «+», а «+» на «−».
Вот еще одна вещь, которую можно показать на примере доски-качалки: вы можете менять две части уравнения местами:
Скобки
Давайте пока остановимся на варианте 7 = 4 + 1 + 2. Предположим, что нам нужно знать, чему равно число 14. Для этого умножаем 7 на 2, но умножать также следует и другую часть уравнения. Поскольку с правой стороны стоят три числа, каждое из них необходимо умножить на 2 вот так:
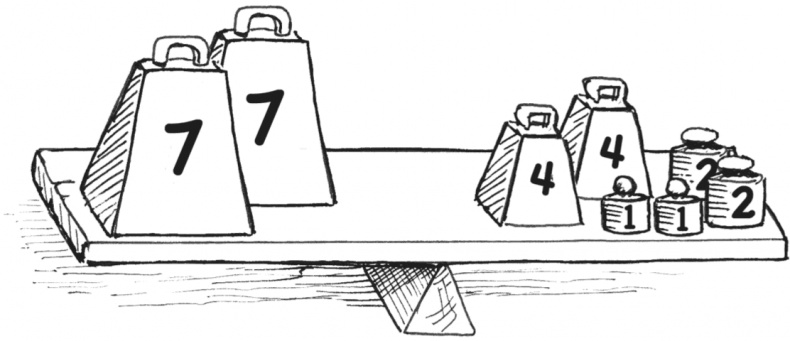
Как видите, мы заключили все числа с правой стороны в скобки. Можно было записать это иначе: 2 × 4 + 2 × 1 + 2 × 2, но со скобками получается короче и удобнее. Число 2 перед скобкой называется коэффициентом.
Если перед открывающей скобкой стоит число, то на него умножается все, что находится внутри скобок.
Добавляем буквы
Наверное, вам уже не терпится перейти к решению хитроумных дифференциальных уравнений, однако начнем с малого.
Прогуливаясь по улице, вы неожиданно встречаете Малькольма, который пребывает в легком шоке. Он только что водил маму в кофейню Barstucks, где они выпили по чашке кофе, и в результате из 10 фунтов, которые он брал с собой, осталось всего 1,20 фунта. Сколько же стоила каждая чашка? Вот что нам известно:
10 фунтов минус цена двух чашек кофе = 1,20 фунта
Мы сэкономим массу типографской краски, если обозначим цену одной чашки кофе буквой c. Из этого следует, что цена двух чашек кофе составит 2 × c, но для удобства мы просто напишем 2c.
Что ж, давайте составим уравнение и посмотрим, как быть дальше.
Нам нужно, чтобы слева от знака равенства была только буква c. Для начала перенесем 10 фунтов на другую сторону, поменяв знак на минус:
Минус перед 2c выглядит не слишком привлекательно, поэтому избавимся от него, умножив обе части уравнения на (−1). В результате каждый знак «+» поменяется на «−», а каждый знак «−» на «+»:
Теперь подсчитаем 10 − 1,20 = 8,80, тогда
Поскольку нам нужна только одна с, разделим обе части на 2, и ответ готов:
