Можно подумать, что 44,8 сильно отличается от 33 нашего грубого подсчета. Но он здесь нужен в основном для того, чтобы убедиться, что запятая в ответе поставлена там, где надо, а то со всеми этими нулями запутаться ничего не стоит. Если бы получился ответ 4,488 дюйма или 0,04488 дюйма, то было бы ясно, что где-то ошибка!
Степени и корни
Большинство из нас никогда не используют степени и корни в повседневной жизни, разве что при расчетах площадей и объемов (о чем мы поговорим немного позже). Однако если вы занимаетесь конструированием гоночных автомобилей или собираетесь слетать в космос, степени и корни понадобятся для расчета скоростей, ускорений, тормозных путей и потребления топлива.
Квадраты и квадратные корни
Мы уже встречались с квадратами чисел в таблице умножения. Квадраты обычно связаны с расчетом геометрических площадей, и обозначают их по-разному: 7 в квадрате – то же самое, что и 7 × 7. Это также можно записать как 7², иначе говоря, 7 в степени 2. Однако, как ни называй, все равно результат равен 49.
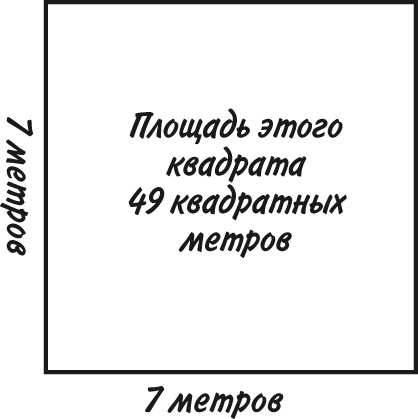
А теперь предположим, что у нас есть число 49 и нужно произвести обратное действие, то есть узнать, какое число, будучи умноженным само на себя, даст 49. Это называется квадратный корень из 49 и записывается как √49, или как 49½, то есть 49 в степени ½. Но что бы вы ни предпочли, в результате все равно получится 7. (Кроме того, квадратным корнем из 49 может быть число −7, поскольку перемножение двух отрицательных чисел даст положительное число.)
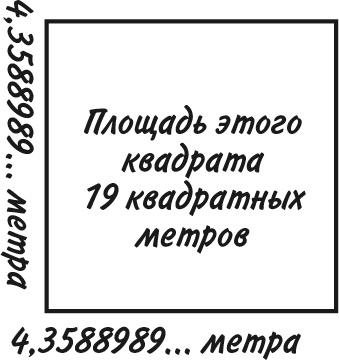
Легче всего извлекать квадратные корни из квадратов целых чисел, таких как 1, 4, 9, 16 и 25, поскольку в этом случае получаются целые значения. С другими числами все куда сложнее. Например, 19 не является квадратом целого числа; тогда какой будет длина каждой стороны квадрата площадью 19 квадратных метров?
Ответ: √19, но сколько это? Мы знаем, что √16 = 4 и √25 = 5, следовательно, квадратный корень из 19 должен дать значение где-то между 4 и 5.

Вычисление корня с помощью карандаша и бумаги требует определенной умственной гимнастики, так что вполне простительно вооружиться калькулятором. Нажимаем клавиши ‹19 √› и получаем 4,3588989… Это десятичная, бесконечно тянущаяся дробь без повторяющихся сочетаний цифр. Такие числа называют иррациональными. Все квадратные корни, которые не являются целыми числами, иррациональны.
Другие степени и корни
Степени могут быть любыми. Помимо квадратов вы еще, скорее всего, столкнетесь только с кубами, например 6³ = шесть в степени три = 6 × 6 × 6 = 216. Кубы используют в основном при вычислении объемов, в простейшем случае – объема кубического сосуда (все стенки которого – квадраты).
Процесс, обратный возведению в куб, называется извлечением кубического корня и обозначается так же, как извлечение корня квадратного, но рядом со значком корня ставится маленькая цифра 3, так, как здесь:
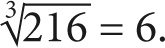
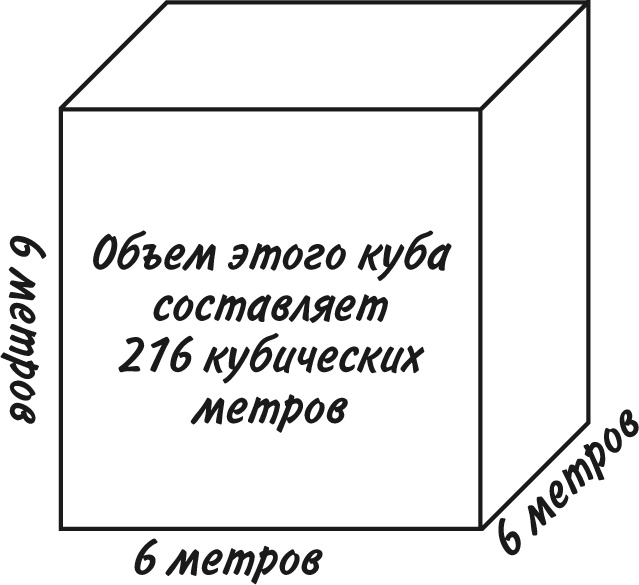
Стало быть, если нам известно, что объем кубического сосуда – 216 кубических метров, то длина каждой его стороны равна кубическому корню из 216, то есть 6 метрам.
Если степень отрицательна, на число под степенью нужно делить. Например, 10−3 – десять в степени минус три. Это то же самое, что и
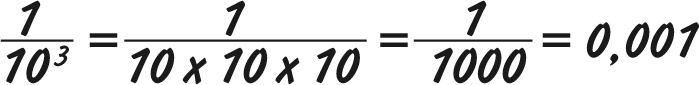
Отрицательные степени часто используют при работе с очень большими или крайне малыми числами, и об этом мы поговорим в следующем разделе.
Нормальная форма
Масса Земли примерно равна 6 000 000 000 000 000 000 000 000 кг.
Официальное название этого числа – шесть септильонов, хотя «шесть с двадцатью четырьмя нулями на конце» звучит понятнее. Можно выразить это не словами, а числами так:
Масса Земли составляет примерно 6 × 1024 кг
Предположим, нам нужно вычислить, сколько будет 6 × 10³. Это то же самое, что и 6 × 1000, поэтому сдвинем 6 на три знака влево и получим 6000. Аналогично 6 × 1024 означает 6 с 24 нулями на конце.
Если вы хотите выразить вес точнее, вместо одной цифры, такой как 6, следует взять десятичную дробь с одним знаком перед запятой и умножить на степень десятки, вот так:
Масса Земли равна 5,9736 × 1024 кг
Это называют записью числа в нормальной форме. Хотя в десятичной дроби гораздо больше цифр, чем одна, множитель × 1024 остался прежним. Умножая на 1024, мы все так же сдвигаем цифры на 24 знака влево, заполняя пустоты нулями. Поскольку цифры 9736 уже занимают четыре знака, просто добавим 20 нулей и получим массу: 5 973 600 000 000 000 000 000 000 кг.
Нормальную форму можно также использовать для очень маленьких чисел.
Масса одного атома водорода равна 1,67 × 10−27 кг
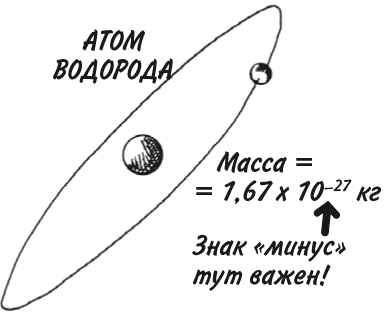
На первый взгляд кажется, что масса атома водорода больше массы Земли. Но это не так. И все благодаря крошечному знаку «минус», из‑за которого мы делим, а не умножаем. Поэтому × 10−27 – это то же самое, что и ÷ 1027, а значит, нужно передвинуть все цифры на 27 знаков вправо.

