Норма, проект, технология, методика, метод. Вслед за О.С. Анисимовым под нормой мы понимаем любую абстракцию, применяемую для организации деятельности: цель, проект, метод и т. п. Под проектом – представление о результате, вместе с представлением о способах его достижения и порядке их расположения во времени. Начиная с этого момента, мы отходим от определений О.С. Анисимова, сохраняя основной принцип их формирования: построение иерархии норм с помощью последовательного абстрагирования понятия «проект». Так, обобщая содержание некоторого набора проектов (каждый из которых имеет дело с уникальным участком деятельности), мы получаем типовой проект, который для наших целей удобно назвать технологией. На более высоком уровне абстракции находится метод, который по степени «очищенности» от конкретики аналогичен математическим объектам и является некоторым алгоритмом, оперирующим понятиями высокой степени общности. Например, метод ограниченного хаоса, о котором будет сказано ниже, выступает алгоритмом, объединяющим понятия «пространство», «функция полезности», «порядок», «хаос», «ограничение». Наконец, методика – это промежуточное звено между методом и технологией. Точное проведение границ в описанной иерархии норм («с какого уровня конкретизации методика превращается в технологию?») для нас в данный момент не принципиально, важно лишь продемонстрировать характер их взаимосвязи.
Цель, задача, проблема, надцель. Под целью будем понимать предписывающее представление о результате некоторой деятельности. Ей параллельна задача как описание исходной ситуации деятельности. Под задачной ситуацией О.С. Анисимов понимает такую, в которой существует некая абстракция (рис. 1, уровень А), с соответствующей конкретикой (уровень К), и в этой конкретике есть пустота, ущербность, требующая заполнения некоторым конкретным объектом. Иначе говоря, в конкретике есть искомое (на рис. 1 место для него заштриховано), в абстракции есть соответствующее ему неизвестное. Например, конкретика: «В первом автобусе было неизвестное количество человек, во втором на 10 человек больше, всего было 50 человек»; соответствующая абстракция: х+х+10 = 50. Здесь х – неизвестное, 20 человек – искомое.
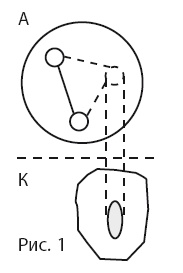
Другой пример задачной ситуации: необходимо создать отдел маркетинга. В роли изменяемой (достраиваемой, ущербной) конкретики здесь выступает фирма, в роли абстракции – некая модель фирмы, в которой присутствует отдел маркетинга. На этом примере хорошо видна связь задачи и цели: задача как описание нынешнего ущербного состояния конкретики содержит в себе цель как описание будущего желаемого состояния конкретики, достроенной до требуемого состояния.
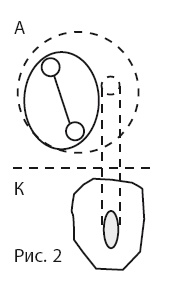
Проблемная ситуация – это ситуация, в которой имеющиеся абстракции неадекватны конкретике (рис. 2), поэтому не существует очевидного неизвестного, или, иначе говоря, невозможно поставить ясную цель, поскольку неизвестно, в чем именно ущербность конкретики и какое ее состояние является желаемым. Лучше всего эта ситуация описывается фольклорным «Пойди туда, не знаю куда, принеси то, не знаю что», а если говорить о современности, именно в проблемной форме часто формулируется заказ на консультирование: «В фирме все плохо, что именно плохо – непонятно, но нужно сделать так, чтобы стало хорошо».
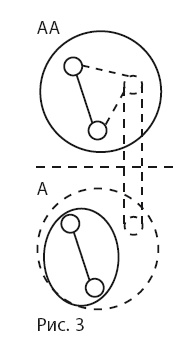
Нетрудно заметить, что если мы имеем некий уровень абстракции АА (рис. 3), на котором возможно абстрактное описание ситуации более конкретного уровня А, то проблемная ситуация является задачной, но сдвинутой на один уровень абстрактности выше. Как задаче соответствовала цель, так и проблеме можно поставить в соответствие надцель – некое описание будущего состояния, сформулированное на уровне АА. Например, проблема «тяжелое положение на южных границах» дает надцель «умиротворить южные провинции», которая может воплощаться в очень различные цели уровня А («разбить войско повстанцев», «склонить вождей повстанцев к миру» и т. п.) и, соответственно, давать различные задачи. Отметим, что термин «надцель» мы заимствовали из ТРИЗ, скорее даже из ТРТЛ (теории развития творческой личности), которая рекомендует творческому человеку ставить себе ДЦ (достойную цель жизни), но кроме упорной работы на ее достижение рассматривать также надцели и переходить к ним по мере появления учеников, включающихся в работу над исходной целью.
Решение проблем. Решение проблемы, как видно из ее определения, распадается на два этапа. Первый – депроблематизация, т. е. превращение проблемы в задачу. Второй – решение задачи. Из сказанного о проблеме как задаче более высокого уровня абстрактности следует, что естественным способом решения проблемы в ситуации неадекватности теории практике является выход на уровень метатеории и достройка теории с ее помощью. О.С. Анисимов считает такой метатеорией общую теорию деятельности (системомыследеятельностную методологию), которая позволяет преодолеть ограничения предметных дисциплин, создающие проблемы при их применении.
В качестве другого примера метатеории можно привести ТРИЗ, благодаря использованию закономерностей уровня АА (философских: противоречие как двигатель развития; близких к математическим: понятие ИКР) позволяющей направленно действовать в ситуациях, являющихся для инженерной науки (дисциплины уровня А) проблемными. Упоминавшаяся неадекватность модели уровня А практике уровня К здесь заключается в исчерпании обычных инженерных методов оптимизации системы на каком-то этапе ее развития, в невозможности дальнейшего развития системы с помощью поиска компромиссов между противоречивыми требованиями к ней.
Между прочим, отсюда понятна обсуждавшаяся выше единственность решения в проблемных ситуациях. Если инженерное (или прожективное) решение задачи допускает различные степени приближения конкретики к предписанной абстракции (есть количественная мера достижения цели), то тризовское (стратегическое) решение дискретно, связано с выходом на новый уровень понимания, формированием новой целостности на уровне А. Выше мы для простоты понимания говорили о достройке модели уровня А, что наводит на мысль о сохранении прежней целостности, к которой просто добавлен новый элемент. Реально же решающим моментом перехода к новой абстракции уровня А является скачкообразное формирование новой целостной модели из обломков старой и массы новых фактов, не вписывавшихся в старую модель. Это тот скачок, который Томас Кун называет сдвигом парадигмы (paradigm shift), а Стивен Кови удачно сравнивает с тем моментом разглядывания забавной картинки «Изображена здесь молодая женщина или старушка?», в который факты (линии, точки), прежде складывавшиеся для человека в одну несомненную картину (например, «старушка»), внезапно приобретают совершенно другое значение (нос старушки вдруг оказывается подбородком молодой женщины и т. д.), и он переходит уже к новой целостной картине, новой интерпретации фактов. Мы показали причины дискретности решения в проблемной ситуации, в следующем разделе покажем возможные причины единственности.





