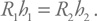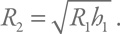Теперь нам надо правильно сформулировать задачу на качественном уровне. Мы знаем, что самые высокие горы на Земле имеют высоту несколько километров. Давайте положим предельную высоту равной 10 км. Если гора будет более высокой, то породы в ее основании не выдержат давления, и гора осядет. Давление (обозначим его P) равняется частному от деления силы на площадь (обозначим ее S): P = F / S. Сделаем разумное предположение, что критическое давление будет одним и тем же для всех космических тел, интересующих нас. Запишем равенство критического давления в двух ситуациях:
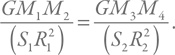
Слева – давление в основании горы массой M2 на первой планете с массой M1 и размером R1, а справа – давление в основании горы массой M4 на второй планете с массой M3 и радиусом R2.
Теперь, чтобы рассчитать силу, нам надо знать массу горы. Представим себе гору как конус. Его масса пропорциональна объему. Математика дает нам возможность рассчитать объем конуса. Он пропорционален произведению высоты (h) на площадь основания:
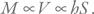 Нам нужно получить давление, таким образом, площадь основания не войдет в ответ.
Нам нужно получить давление, таким образом, площадь основания не войдет в ответ.
Масса планеты пропорциональна ее объему. Объем шара пропорционален кубу радиуса:
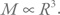 Подставив это в формулу и сократив все, что можно сократить, мы получим простое соотношение:
Подставив это в формулу и сократив все, что можно сократить, мы получим простое соотношение:
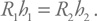
Нас интересует случай, когда второе тело имеет заметно несферическую форму, т. е. высота горы на второй планете сопоставима с радиусом, т. е. R2 = h2. Соответственно, для оценки критического радиуса тела, которое может начинать заметно отклоняться от сферической формы, получаем:
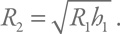
Подставим в качестве R1 радиус Земли, в качестве h1 – предельную высоту гор на Земле и получим: R2 ≈ 250 км.
Эта простая оценка прекрасно соответствует действительности: спутники и астероиды с диаметром менее нескольких сотен километров уже могут иметь заметно несферическую форму (примером может служить спутник Сатурна Прометей), а более крупные (как, например, Церера) – округлую. Разумеется, чем меньше размер, тем заметнее может быть отклонение от правильной формы. 500-километровые Веста и Паллада лишь слегка несферичны, а 100-километровая Лютеция уже сильно отклоняется от шарообразной формы.
Таким образом, воспользовавшись простыми геометрическими формулами (объем конуса, объем шара) и записав наши предположения о физике тела в математической форме, мы сумели в рамках простой модели рассчитать предельный размер тела, которое своей гравитацией может заметно сглаживать рельеф на своей поверхности. Конечно, можно проводить более детальные и точные расчеты, учитывая в первую очередь разницу во внутреннем строении различных тел (спутники и астероиды могут состоять из менее плотных пород, чем земная кора). Но прелесть именно в том, что уже без этих деталей можно получить вполне разумный результат.
Приложение 10
Гипотезы в астрофизике
Ньютону принадлежит известная фраза: «Гипотез не измышляю». Что здесь имеется в виду? Ведь ученые постоянно работают с гипотезами. На мой взгляд, речь идет о том, что не надо придумывать «чайник Рассела»
[137], но не более того. Не имея никаких дополнительных данных, Ньютон считал преждевременным рассуждать о природе гравитации. Слишком мало информации было в то время (равно как век и даже два века спустя), чтобы высказывать разумные гипотезы, которые можно было бы проверять или хотя бы развивать таким образом, чтобы это выходило за рамки общефилософских рассуждений. Такой подход, однако, не мешал сэру Исааку развивать и защищать корпускулярную природу света – об этом явлении в его время знали гораздо больше, и в данной области гипотезы были вполне уместны.
Таким образом, важно, насколько гипотеза обоснована и что из нее можно извлечь. Возьмем в качестве примера вопрос о форме Земли. С одной стороны, совсем банально-бытовой опыт говорит, что Земля плоская (ну, может, слегка выпуклая, как плоско-выпуклая линза). С другой – философской – точки зрения греки могли бы начать обсуждать платоновы тела (куб, икосаэдр, октаэдр, тетраэдр, додекаэдр). Однако существовал целый комплекс (sic!) данных, говорящих о том, что Земля имеет шарообразную форму.
Кроме всяких косвенных и частичных данных, а также аналогий, имелся ключевой факт (к понятию косвенных данных и ключевых фактов мы еще вернемся в конце главы), связанный с лунными затмениями. Конфигурация тел при этом событии всем известна: Земля располагается точно между Луной и Солнцем. Таким образом, наблюдая край земной тени, мы можем определить ее форму. Разумеется, чтобы быть уверенным, что мы не имеем дело лишь с одной проекцией Земли, нам надо пронаблюдать несколько затмений, когда Луна находится в разных участках неба. А лучше провести еще наблюдения из разных точек земной поверхности, в том числе и одновременно. К счастью, лунные затмения происходят не так уж редко и видны сразу на большой территории, поэтому задача вполне выполнима. Мы можем убедиться в том, что край земной тени всегда представляет собой дугу окружности. Значит, Земля – шар.
Теперь, воспользовавшись этой гипотезой, можно ни больше ни меньше как измерить размер Земли! Это сделал Эратосфен в III веке до н. э. Если у нас есть шар и мы можем достаточно точно измерить отрезок дуги большого круга
[138], зная, какому углу она соответствует, то немедленно получим радиус. Углы измерялись по высоте Солнца в полдень, а длина – по пройденному пути в направлении север-юг. В результате была получена величина, достаточно близкая к верной. Иначе говоря, гипотеза была не чисто умозрительной и привела к важному результату (с потенциальными возможностями практического применения; например, можно было рассчитать примерную длину пути при кругосветном путешествии).



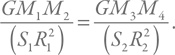
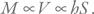 Нам нужно получить давление, таким образом, площадь основания не войдет в ответ.
Нам нужно получить давление, таким образом, площадь основания не войдет в ответ.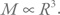 Подставив это в формулу и сократив все, что можно сократить, мы получим простое соотношение:
Подставив это в формулу и сократив все, что можно сократить, мы получим простое соотношение: