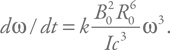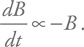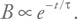В деталях механизм излучения пульсаров известен плохо, но его можно наглядно проиллюстрировать и даже получить качественно верное выражение для светимости, пользуясь очень простыми соображениями.
Мы уже рассматривали вращающийся шар и помним, что каждая частица шара вращается со скоростью, равной ωr, где r – расстояние от оси вращения. Иначе говоря, чем дальше частица, тем быстрее она вращается. Теперь представьте, что из шара торчат линии магнитного поля. Они жестко связаны с внешними слоями нейтронной звезды, так что вращаются с той же самой частотой (т. е. с тем же периодом). Теперь, как бусинку на проволоку, мы помещаем на линию магнитного поля частицу. Ее скорость вращения также равна ωr. Но мы уже рассматриваем вращение вне нейтронной звезды, а потому с ростом расстояния можем добраться до скорости света!
Ни частица, ни магнитная линия не могут вращаться со скоростью, превышающей световую. Значит, есть критическое расстояние, на котором замкнутая магнитосфера, заполненная заряженными частицами, перестает существовать. Поверхность, отстоящую от оси вращения на Rl = c / ω, называют световым цилиндром. Вне светового цилиндра будут присутствовать только электромагнитные волны и релятивистские частицы, улетающие от нейтронной звезды. Они-то и уносят энергию вращения, т. е. тормозят пульсар. Теперь, качественно представив себе физическую картину, мы готовы получить формулу для светимости пульсара.
Светимость – это количество энергии, испускаемое в единицу времени. Энергия у нас запасается в магнитосфере внутри светового цилиндра, а характерное время испускания – период вращения (напомним, что P = 2π / ω). Сколько же у нас есть энергии? Снова воспользуемся произведением плотности энергии магнитного поля B2 / 8π на объем, но теперь возьмем объем магнитосферы, а величину поля – на световом цилиндре (нас интересуют самые внешние области с большим объемом, которые могут участвовать в процессе излучения). С расстоянием поле спадает как куб радиуса. Пусть поле на поверхности нейтронной звезды с радиусом R0 равно B0. Тогда для энергии получим:
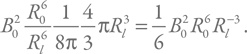
Подставив выражение для радиуса светового цилиндра Rl = c / ω, получим энергию (пренебрегая численными множителями):
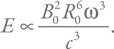
Теперь, чтобы получить светимость, остается разделить это на характерный период. Получим:
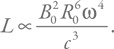
Таким образом, светимость больше для нейтронных звезд с более сильным полем, но, самое главное, она очень быстро спадает с ростом периода: пульсар с периодом 1 с излучает в 10 000 раз меньше, чем при периоде 0,1 с.
Мы уже выписывали уравнение для энергии вращения: Iω2 / 2. Возьмем производную по времени от этой величины. Момент инерции не меняется со временем, поэтому для темпа потерь энергии вращения получим выражение
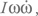 где точка сверху обозначает производную по времени
где точка сверху обозначает производную по времени
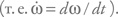 Приравняв эту величину к светимости (добавим в формулу для светимости безразмерный коэффициент
[120] k, чтобы учесть отброшенные безразмерные множители), получим:
Приравняв эту величину к светимости (добавим в формулу для светимости безразмерный коэффициент
[120] k, чтобы учесть отброшенные безразмерные множители), получим:
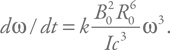
Можно теперь заменить угловую частоту на период и проинтегрировать. Получим, что период нейтронной звезды на стадии радиопульсара возрастает как квадратный корень из времени. Иными словами, если молодая нейтронная звезда возрастом 100 лет имеет период 0,1 с, то к миллиону лет этот период возрастет до 10 с. Это примерно отражает поведение типичного радиопульсара.
Разобравшись с выделением энергии вращения и некоторыми ее свойствами, перейдем к выделению энергии магнитного поля. Да-да, это возможно, ведь поле порождается электрическими токами. А энергию токов мы используем постоянно.
У нейтронной звезды нет батареек, и она не подключена к розетке, поэтому текущие в ней токи со временем затухают, а из-за этого уменьшается магнитное поле. Затухание тока связано с электрическим сопротивлением. Легко сообразить, что сильные токи будут затухать сильнее, а это означает, что сильные поля быстрее уменьшаются. Немного упростив ситуацию, мы можем представить это в виде такой несложной формулы:
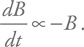
Она показывает, что темп изменения поля (он стоит слева) прямо пропорционален величине поля (она стоит справа), а знак минус указывает на то, что поле со временем становится меньше. Решая это уравнение, мы получим, что поле уменьшается экспоненциально с некоторым характерным временем τ (это время зависит от коэффициентов в уравнении, которые мы обсуждать не будем):
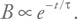
Энергия тока в таком случае выделяется постепенно, переходя в тепло. Мы с этим постоянно сталкиваемся в быту (пока я пишу эти слова, вскипел чайник, а руками я чувствую, как нагрелся мой ноутбук, – все из-за электрических токов и сопротивления!). Но можно выделять энергию токов быстро – в результате короткого замыкания.
Не пытайтесь проверить, но короткое замыкание – очень эффективный способ быстрого выделения большой энергии. Пожалуй, только так в домашних условиях можно легко оплавить не слишком легкоплавкий металл. Именно с помощью природного электрического пробоя в фильме «Назад в будущее» смогли решить проблему, возникшую из-за поломки ядерного реактора. Если устроить короткое замыкание в коре нейтронной звезды, то можно выделить заметную долю от полной энергии магнитного поля в компактном объекте. Так работают магнитары.
Во время самой мощной из известных магнитарных вспышек пиковая светимость составила примерно 1047 эрг/с. Это более чем 10 000 000 000 000 светимостей Солнца. Намного больше светимости целой галактики! А источником был всего лишь 10-километровый шарик.
Даже если энерговыделение не связано с вращением или диссипацией энергии токов, магнитное поле все равно может оказаться «при деле». Так происходит в аккрецирующих нейтронных звездах.
5Б. Аккрецирующие объекты
В приложениях 3 и 4 мы уже обсудили некоторые особенности процесса аккреции и смогли оценить его высокую эффективность, если вещество падает на массивные компактные объекты. В случае аккреции на поверхность нейтронной звезды каждый грамм вещества выделяет огромную энергию, которую можно оценить как GM / R0, где R0– радиус нейтронной звезды, а M – ее масса. Подставим типичные для этих компактных объектов параметры и получим 1020 эрг на 1 грамм
[121]. Это примерно 10 % от mc2! В десять с лишним раз больше, чем у термоядерных реакций в недрах Солнца. Неудивительно, что аккрецирующие нейтронные звезды являются мощными источниками. Теперь посмотрим, какие особенности есть при аккреции на нейтронные звезды, обладающие магнитным полем.



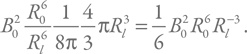
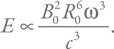
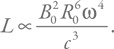
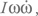 где точка сверху обозначает производную по времени
где точка сверху обозначает производную по времени
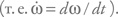 Приравняв эту величину к светимости (добавим в формулу для светимости безразмерный коэффициент
Приравняв эту величину к светимости (добавим в формулу для светимости безразмерный коэффициент