Начнем мы, как ни странно, с принципа неопределенности Гейзенберга и корпускулярно-волнового дуализма. Легенда гласит, что в разговоре с Яковом Борисовичем Зельдовичем Владимир Наумович Грибов высказал следующую мысль. Возникает парадокс, если мы применим принцип Гейзенберга к черным дырам. С одной стороны, мы говорим, что из них ничего не вылетает, а с другой – как же мы локализуем в маленькой черной дыре частицу, длина волны которой превосходит размер черной дыры? Иными словами, в некотором смысле квантовая механика вступает в противоречие с ОТО. Грибов полагал, что «квантовая механика победит».
Предельный масштаб, на котором мы можем локализовать частицу, связан с ее комптоновской длиной волны:
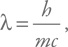
где m – масса частицы.
Что же это за длина волны? Это можно пояснить таким образом (хотя в таком упрощенном комментарии есть элемент передергивания). Каждой длине волны соответствует частота, которую можно рассчитать, используя скорость распространения волны. В данном случае – скорость света: ν = c /λ. С одной стороны, если мы рассматриваем волну, то энергия частицы будет равна E = hν. С другой – энергия частицы при такой предельной локализации будет порядка ее энергии покоя: E = mc2. Таким образом, hν = hc /λ = mc2. А отсюда мы сразу получаем, что
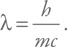
Принцип неопределенности Гейзенберга записывается таким образом:
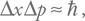
где Δx – неопределенность координаты, а Δp – неопределенность импульса частицы.
В нашем рассуждении существенно, что мы пытаемся локализовать частицу по координате с точностью порядка ее комптоновской длины волны. Это приведет к тому, что неопределенность импульса будет порядка Δp = mc (именно поэтому выше мы могли использовать скорость света при сопоставлении частоты и длины волны). Тогда для Δx получим:
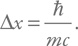
Таким образом, эта величина равна комптоновской длине волны, деленной на 2π. Эту величину называют приведенной комптоновской длиной волны и записывают так:
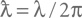 (а величину
(а величину
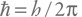 называют приведенной или редуцированной постоянной Планка).
называют приведенной или редуцированной постоянной Планка).
Теперь получим оценку температуры черной дыры. С одной стороны, пределом для «вылезания» частицы из дыры будет равенство диаметра черной дыры и приведенной комптоновской длины волны (напомним, что мы всего лишь даем некую иллюстрацию, на самом деле никакие частицы из черной дыры не «вылупляются», они не пересекают горизонт «оттуда сюда», а возникают «с нашей стороны» из-за изменений параметров вакуума, связанных с нестационарностью горизонта). С другой стороны, при излучении у нас есть равенство для тепловой энергии частицы и энергии кванта:
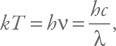
где длина волны – это комптоновская длина.
Приведенную длину мы оценили как удвоенный радиус черной дыры, для которого используем стандартную формулу Шварцшильда:
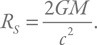
Таким образом получаем:
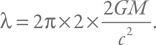
Теперь соберем все вместе и получим выражение для температуры:
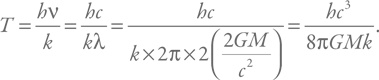
Формула лишь коэффициентом π отличается от точного значения. Разумеется, это совсем не строгий вывод, и, только зная аккуратно полученный правильный результат, можно потирать руки, радуясь тому, что мы таким простым способом получили столь фундаментальную формулу. Тем не менее приятно, что можно построить такую наглядную цепочку рассуждений.
Отметим, что при уже упоминавшейся массе 1026 г температура будет примерно равна современной температуре реликтового излучения, заполняющего всю вселенную (в прошлом температура была выше). Так что, даже если мы сейчас поместим черную дыру в совсем пустую область космоса, она все равно будет расти за счет поглощения фотонов реликта при массе больше 1026 г.
Итак, у нас есть температура, значит, в первом приближении мы можем посчитать светимость
[112]. Для теплового излучения сферы радиуса R она рассчитывается по формуле
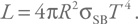
Напомним, что постоянная Стефана – Больцмана равна:
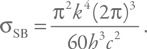
В качестве радиуса излучающей поверхности подставим шварцшильдовский радиус. Затем светимость запишем в таком виде:
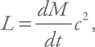
т. е. мощность излучения определяется темпом потери массы. Тогда мы сможем записать:
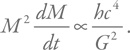
Проведем интегрирование от начальной массы M до нуля (полное испарение) и для времени полного испарения получим:
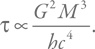
Точная формула выглядит так:
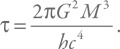
Мы снова с точностью до численных коэффициентов получили верный результат!
Можно получить его и несколько иначе. Пусть энергия уносится квантами электромагнитного излучения (напомним, что на первых этапах испарения, пока температура недостаточно велика, частицы не рождаются – только излучение). Энергия одного кванта равна
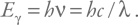 Характерное время испускания составляет Δt = λ/ c. Запишем вначале такое выражение (оно соответствует светимости L):
Характерное время испускания составляет Δt = λ/ c. Запишем вначале такое выражение (оно соответствует светимости L):



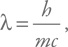
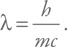
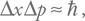
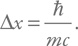
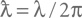 (а величину
(а величину
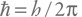 называют приведенной или редуцированной постоянной Планка).
называют приведенной или редуцированной постоянной Планка).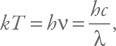
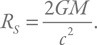
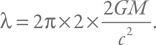
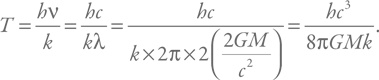
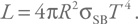
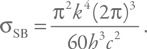
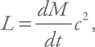
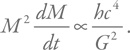
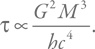
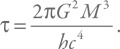
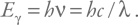 Характерное время испускания составляет Δt = λ/ c. Запишем вначале такое выражение (оно соответствует светимости L):
Характерное время испускания составляет Δt = λ/ c. Запишем вначале такое выражение (оно соответствует светимости L):