где δφ – угол, на который отклоняется свет, М – масса гравитационной линзы, а r – минимальное расстояние между траекторией светового луча и центром линзы.
Гравитационное линзирование встречается в астрономии в самых разных вариантах. В роли источника может выступать далекий квазар, а в роли гравитационной линзы – массивная галактика. Или же источником является далекая сверхновая, и ее свет линзируется на скоплении галактик. Мой любимый пример таков. Источником является аккреционный диск в далекой активной галактике, а его излучение линзируется на отдельных звездах более близкой галактики на луче зрения
[106]. В такой поразительной ситуации мы можем измерить параметры диска (по сути, определить, как его температура меняется с радиусом).
Однако здесь нас будет интересовать случай так называемого микролинзирования. Микро-, потому что линза относительно легкая, это объект звездной массы. Источником в такой ситуации обычно является звезда нашей Галактики, и, конечно, в ней же находится и линза.
Если мы смотрим на какую-то случайно выбранную звезду, то понадобятся сотни тысяч лет, пока еще какой-то умеренно массивный объект (другая звезда, бурый карлик или компактный остаток) пролетит столь близко к лучу зрения, что вызовет заметный эффект.
Какие эффекты могут возникать при таком пролете? Во-первых, это просто смещение видимого положения звезды-источника. Такой случай называют астрометрическим линзированием. Наблюдать эффект очень трудно, так как он мал. Но иногда это удается (если знать, куда смотреть с помощью крупных телескопов), а кроме того, спутник Gaia вскоре должен представить много данных по таким явлениям. Но более известным является так называемое фотометрическое микролинзирование, к которому мы и перейдем.
Гравитационная линза всегда работает таким образом, что усиливает блеск источника. Для этого он должен оказаться на небольшом угловом расстоянии от линзы – внутри так называемого конуса Эйнштейна. Если считать, что источник расположен гораздо дальше линзы, то этот кружок на небе характеризуется угловым радиусом, вычисляемым по очень простой формуле (вот только вывод ее не так уж прост, и здесь мы его приводить не будем):
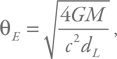
где dL– расстояние от наблюдателя до линзы, а М – ее масса.
Если подставить звездную массу и расстояние порядка нескольких тысяч световых лет, то мы получим угол примерно в несколько сотых угловой секунды. Вероятность того, что одна из звезд попадет в такой кружок, крайне мала, поэтому и надо ждать сотни тысяч лет, пока это произойдет. Но если уж такое случилось, то блеск звезды возрастает в несколько раз, что легко заметить.
С появлением цифровых приемников излучения, чья главная характеристика – число мегапикселей, астрономы научились сразу измерять блеск большого числа звезд. Это дало возможность начать специальные программы наблюдений, охотящихся за случаями микролинзирования. Сейчас счет зарегистрированным событиям идет на многие тысячи.
А что же черные дыры? Насколько часто в роли линзы может выступить такой объект? Чтобы в этом разобраться, нам надо сравнить количество и массы обычных звезд, черных дыр, а также нейтронных звезд и белых карликов
[107].
Начнем с масс. Наблюдения говорят нам, что средняя масса белых карликов составляет примерно 0,6 солнечных, нейтронных звезд – 1,3, а черных дыр – 5–10. Для обычных звезд мы снова воспользуемся начальной функцией масс в виде:
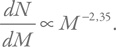
Масса звезд в интервале dM в окрестности какой-то массы M равна просто произведению этой массы на dN. Соответственно, полная масса звезд будет пропорциональна интегралу
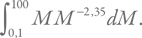
А полное количество звезд, как и выше в приложении 4А, – интегралу
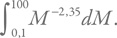
Коэффициент пропорциональности одинаковый. Соответственно, средняя масса звезды, равная отношению массы всех звезд к их количеству, будет отношением этих интегралов. Учитывая, что нижний предел гораздо меньше верхнего, а под интегралом стоят отрицательные степени, по модулю большие единицы, мы получим, что отношение примерно равно
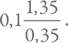 . Это дает 0,38. Обычно используется средняя звездная масса, равная 0,3, поскольку в качестве нижнего предела подставляется неокругленное значение 0,08 солнечных масс.
. Это дает 0,38. Обычно используется средняя звездная масса, равная 0,3, поскольку в качестве нижнего предела подставляется неокругленное значение 0,08 солнечных масс.
Итак, звезды в среднем вдвое легче белых карликов, примерно в пять раз – нейтронных звезд и примерно в 20 раз – черных дыр. Это важно, так как для этих объектов будут пропорционально квадратному корню из массы изменяться параметры конусов Эйнштейна.
Теперь оценим относительное количество этих четырех типов объектов. Выше, в приложении 4А, мы уже сравнивали количество черных дыр с количеством звезд. Аналогичным способом, меняя пределы интегралов, можно получить, что нейтронных звезд примерно в 5 раз, а белых карликов раз в 20 больше, чем черных дыр.
Собирая все вместе, получаем, что почти 90 % случаев линзирования должны быть связаны с обычными звездами
[108]. Примерно в 10 % случаев линзами могут являться белые карлики, а вот на долю нейтронных звезд и черных дыр вместе приходится около 1–2 % (вклад нейтронных звезд несколько уменьшается из-за их высокой скорости, так как они быстро покидают диск Галактики). Однако, поскольку случаев линзирования известно уже более десяти тысяч, то и 1 % – это хорошо.



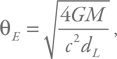
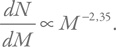
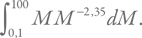
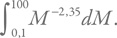
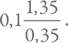 . Это дает 0,38. Обычно используется средняя звездная масса, равная 0,3, поскольку в качестве нижнего предела подставляется неокругленное значение 0,08 солнечных масс.
. Это дает 0,38. Обычно используется средняя звездная масса, равная 0,3, поскольку в качестве нижнего предела подставляется неокругленное значение 0,08 солнечных масс.