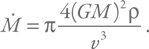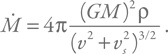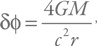В случае аккреции вещества межзвездной среды захватывается газ, поэтому за счет вязкости можно обеспечить довольно эффективный отвод орбитального момента наружу. Взаимодействие частиц газа в потоке будет приводить к переносу орбитального момента прочь от гравитирующего центра, а вещество, потерявшее момент, будет течь в его сторону. Поэтому аккреция начинается, если вещество проникло под радиус гравитационного захвата. Теперь мы можем сделать простую оценку максимального темпа аккреции.
Итак, черная дыра массы M летит со скоростью v сквозь межзвездную среду плотностью ρ. Будем считать, что все вещество, попадающее внутрь радиуса гравитационного захвата, в итоге поглотится черной дырой. Значит, объем поглощенного за единицу времени вещества будет равен объему цилиндра, длина которого равна произведению скорости на интервал времени (не забываем, что он у нас единичный), а площадь основания равна
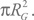 Таким образом, темп аккреции будет равен:
Таким образом, темп аккреции будет равен:
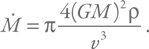
Учет некоторых тонкостей может изменить численный коэффициент, но общие зависимости останутся, и по порядку величины эта оценка верна.
Необходимо сделать один комментарий относительно скорости. Глядя на формулу, кажется, что можно достичь очень высокого темпа аккреции, если черная дыра будет двигаться относительно среды с очень низкой скоростью. Однако необходимо учесть, что частицы среды сами движутся, и в космических условиях эта скорость может быть довольно велика. Хорошей оценкой характерной скорости будет величина скорости звука vs в межзвездной среде, которая в зависимости от комбинации температуры и плотности может составлять от нескольких сотен метров в секунду в самых холодных и плотных областях до десятков километров в секунду. С учетом скорости звука формула немного изменится:
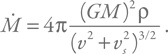
Если мы подставим в формулу типичные значения: ρ = 10–24 г / см3, M = 2·1034 г, а для обеих скоростей возьмем значения 10 км/с (в случае скорости звука это типичное значение, а вот для скорости движения – скорее, нижний предел), то получим примерно 1013 грамм в секунду.
Теперь возникает более сложный момент – посчитать эффективность аккреции, т. е. сколько энергии выделится на грамм вещества, провалившегося в конце концов в черную дыру. И вот тут ясности нет. Дело в том, что поверхность-то у черной дыры отсутствует! Иначе говоря, выделить энергию при контакте с поверхностью невозможно. Значит, все энерговыделение должно идти в потоке. Насколько оно эффективно, в ряде случаев неясно. Если аккрецируемое вещество обладает достаточно большим орбитальным моментом, то вокруг черной дыры формируется аккреционный диск. За счет вязкости (по сути, за счет трения слоев газа друг о друга) энерговыделение достигает больших значений. Именно поэтому мы видим мощное излучение квазаров, блазаров и других активных галактических ядер, а также черных дыр в рентгеновских тесных двойных системах. В том случае, если и при аккреции из межзвездной среды формируется диск, можно рассчитывать на довольно значительную светимость. Давайте попробуем оценить верхний предел для нее.
Поступим очень просто. Оценим гравитационную потенциальную энергию на внутреннем крае аккреционного диска. В случае черных дыр существует важное понятие последней устойчивой круговой орбиты. Для невращающейся вокруг своей оси черной дыры (а мы думаем, что одиночные черные дыры, блуждающие по Галактике, в основном имеют относительно медленное вращение, поскольку раскрутить черную дыру можно в первую очередь мощной аккрецией в тесной двойной системе) радиус такой орбиты равен 6GM/c2, т. е. трем шварцшильдовским радиусам. После достижения этой границы вещество в диске очень быстро «вспираливается» под горизонт. Таким образом, плотность вещества в потоке под критическим радиусом мала, а потому там трудно сгенерировать мощное излучение за счет вязкости. На радиусе гравитационного захвата вещество имеет практически нулевую энергию. Значит, верхний предел на энерговыделение будет примерно равен по модулю потенциальной энергии на последней устойчивой орбите. Воспользовавшись приведенной несколько выше формулой для массы m, получим энерговыделение (mc2 / 6). Это много: каждый грамм будет давать 1,5·1020 эрг. Объединив это с полученной выше оценкой темпа аккреции и немного округлив, получим примерно треть светимости Солнца – довольно заметный источник!
Однако до сих пор одиночные аккрецирующие черные дыры не идентифицированы (здесь я нарочито избегаю слов «не обнаружены», поскольку потом может оказаться, что какие-то из известных слабых источников относятся к данному классу объектов). Расчеты показывают, что в спектре излучения одиночных аккрецирующих черных дыр может быть два максимума: в инфракрасной и рентгеновской области. Соответственно, предпринимались попытки выявить слабые источники с такими свойствами. Проводились специальные поиски в направлениях молекулярных облаков, где выше плотность среды, а значит, выше темп аккреции и, следовательно, светимость. Но все пока безрезультатно.
Вероятнее всего, приведенная выше оценка темпа аккреции завышает реальную величину, а значит, черные дыры будут более слабыми источниками. Однако нет никаких сомнений, что в Галактике блуждают многие десятки миллионов черных дыр звездных масс, потихоньку поглощающих вещество межзвездной среды. При этом выделяется какое-то количество энергии в виде электромагнитного излучения. Стало быть, рано или поздно они будут обнаружены.
А пока есть другой, уже работающий способ открывать одиночные черные дыры.
4Б. Линзирование
Любое тело обладает массой, а значит, искривляет пространство-время вокруг себя. Это сказывается на движении всех объектов в данной области. Разумеется, чем массивнее тело, тем на большем расстоянии оно может оказывать заметное влияние. Нас будет интересовать, как присутствие массивного тела сказывается на распространении электромагнитных волн, и в частности света.
Заметим, что отклонение световых лучей как таковое – это не совсем «изобретение» общей теории относительности. Согласно ньютоновской модели, свет, если представить его себе как поток очень легких частиц (именно так себе представлял свет сам Ньютон), также должен отклоняться, только эффект будет в два раза меньше, чем в ОТО
[105]. Наблюдения смещения положения звезд во время солнечных затмений (а затем и другие многочисленные наблюдения и эксперименты) показали, что верен расчет в рамках ОТО – при небольших углах отклонения работает формула
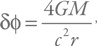



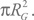 Таким образом, темп аккреции будет равен:
Таким образом, темп аккреции будет равен: