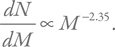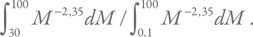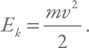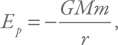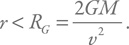4А. Аккрецирующие одиночные черные дыры
Ядра массивных звезд в завершение их эволюции могут превращаться в черные дыры. Точные интервалы начальных масс прародителей этих компактных объектов неизвестны, но для простой оценки предположим, что основная доля звезд, имеющих при рождении массы более 30 солнечных, в конце порождают именно черные дыры
[100]. Далее предположим, что распределение звезд по начальным массам можно описать так называемой солпитеровской функцией
[101]:
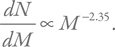
Это означает, что количество звезд dN в небольшом интервале масс шириной dM – от M до (M + dM) – пропорционально массе в степени –2,35, т. е. количество звезд быстро спадает с ростом массы
[102]. Данная зависимость была установлена на основе наблюдений.
В качестве минимальной массы звезды возьмем 0,1Mʘ, а в качестве максимальной – 100Mʘ. Теперь, чтобы посчитать долю звезд с массой более 30 солнечных, нам надо найти отношение двух интегралов:
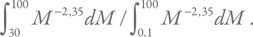
Это отношение примерно равно 0,00045. Учитывая, что за время существования Галактики в ней сформировалось около 300 млрд звезд, мы получим, что сейчас в ней должно быть около 135 млн черных дыр (заметим, что это очень близко к более точным расчетам). Типичная масса таких объектов – 5–10 масс Солнца. Это следует и из теории, и из наблюдения черных дыр в тесных аккрецирующих двойных системах.
При рождении черные дыры, в отличие от нейтронных звезд, в среднем не получают большую дополнительную скорость, связанную с асимметрией взрыва сверхновой (так называемый кик). Значит, они остаются в галактическом диске, и мы можем легко оценить их плотность в солнечной окрестности. Представим диск Галактики в виде цилиндра с радиусом около 15 кпк и толщиной около 1 кпк. Разделив его объем на количество черных дыр, получим объем, приходящийся на один объект, – это около 5000 кубических парсек. Значит, расстояние до ближайшей одиночной черной дыры будет порядка 10 пк.
Таким образом, черных дыр звездных масс в Галактике много, и они могут находиться не так уж далеко от нас. Вопрос в том, как их обнаружить.
В приложении 3 мы обсудили, что аккреция на черные дыры может приводить к выделению значительной энергии. Надо только найти эффективный источник вещества. Если компактный объект одиночный, т. е. бороздит просторы Галактики сам по себе, тогда единственным источником будет межзвездная среда
[103].
Плотность межзвездного вещества вблизи плоскости диска Галактики в солнечных окрестностях не слишком высока – около одного атома водорода в кубическом сантиметре. В молекулярных облаках это значение возрастает в десятки, а то и в сотни раз. Нам нужно оценить, с каким темпом черная дыра может захватывать это вещество.
Чаще всего, когда на популярной лекции заходит речь о черных дырах, выясняется, что хотя бы кто-то из слушателей полагает, что черные дыры – это такие пылесосы, которые «затягивают в себя все и когда- нибудь совсем все и затянут». Это совсем не так.
Действие черных дыр на другие тела определяется гравитацией. Если мимо черной дыры пролетает тело, то нам надо сравнить его кинетическую энергию, связанную с движением относительно компактного объекта, и гравитационную потенциальную энергию, связанную с взаимодействием между телами. Формулу для кинетической энергии все помнят:
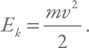
Потенциальную энергию удобно считать отрицательной, и для нее выражение выглядит так:
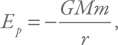
где G – гравитационная (ньютоновская) постоянная, M – масса массивного центрального тела (в нашем случае – черной дыры), m – масса пролетающего тела, а v – его скорость.
Ясно, что если скорость слишком велика, то кинетическая энергия тоже будет велика, и, таким образом, полная энергия, равная сумме кинетической и потенциальной, будет больше нуля, т. е. система будет гравитационно несвязанной. Иными словами, тело пролетит мимо. Точно так же при большом расстоянии между телами – r – потенциальная энергия будет мала, и снова связанная система не образуется. Таким образом, чтобы черная дыра захватила пролетающее тело (им может быть и молекула газа межзвездной среды), надо, чтобы выполнялось некоторое условие
[104]. Вот оно:
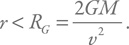
Критическое расстояние RG называют радиусом гравитационного захвата.
Однако мало тело захватить, ведь оно может просто вращаться вокруг черной дыры на устойчивой орбите (как Земля вокруг Солнца или Луна вокруг Земли). Телу нужно избавиться от вращения – потерять орбитальный момент. В системе двух тел такой возможности практически нет (исключение составляют приливы, а в случае черной дыры и атома водорода какие уж тут приливы!). Необходимо, чтобы вокруг центрального массивного объекта вращалось несколько тел, которые могли бы достаточно эффективно обмениваться энергией и орбитальным моментом. Тогда часть из них сможет перейти на более низкие орбиты и в конечном счете выпасть на центральный объект.