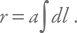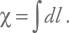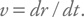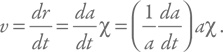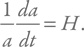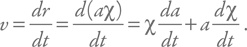Определяя r в какой-то момент времени, мы можем считать масштабный фактор a постоянной величиной (ведь он изменяется только со временем и в каждый момент один и тот же для всей вселенной). Значит,
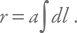
А интеграл от dl равен, по определению, сопутствующему расстоянию:
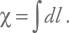
Расстояние r называют собственным. Именно оно показывает, сколько сантиметров (метров, километров, парсек или световых лет) между двумя объектами в данный момент времени. Это расстояние растет в расширяющейся вселенной, что описывается изменением масштабного фактора. Обычно удобно считать, что в настоящий момент a = 1. Соответственно, в прошлом a < 1, а в будущем a > 1.
Теперь, введя все необходимые величины, переходим к выводу закона Хаббла. Определим скорость как производную от собственного расстояния:
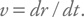
Дальше произведем короткую цепочку простых преобразований, помня, что мы считаем сопутствующее расстояние неизменяющимся:
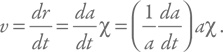
Вспомним, что r = aχ, и введем обозначение:
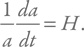
Получаем искомое v = Hr, где H – постоянная Хаббла.
Вот мы и вывели закон Хаббла. Теперь посмотрим на некоторые следствия из него.
Крайне существенно, что в космологии надо использовать общую теорию относительности. Это не та ситуация, где можно обойтись лишь СТО, такая попытка приведет к неправильным результатам и только запутает. Например, скорости в космологии складываются по простому галилеевскому правилу.
Если у нас есть три галактики на одной прямой – 1, 2 и 3, то скорость третьей относительно первой составит:
v13= v12 + v23 = Hr12 + Hr23 = Hr13,
где r13 = r12 + r23.
Это верно для любых скоростей: не только близких к скорости света, но и превосходящих ее.
Кроме участия в космологическом расширении – так называемом хаббловском потоке, галактики могут иметь пекулярные скорости (например, пара галактик может сближаться, как Млечный Путь и Туманность Андромеды). Такие скорости соответствуют изменению сопутствующих координат:
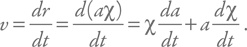
Здесь первое слагаемое – обычное космологическое расширение, а второе связано с пекулярной скоростью. Снова мы имеем дело с простой суммой, какими бы большими ни были скорости.
А они могут быть большими. Если пекулярные скорости не могут превосходить световую, то скорость, связанная с космологическим расширением (именно она входит в закон Хаббла), может быть любой, если расстояние сколь угодно велико. Таким образом, есть расстояние, на котором она сравнивается с c = 300 000 км/с.
Хаббловской сферой называют поверхность, собственное расстояние до которой определяется как r = c / H. Иными словами, в данный момент времени галактики, находящиеся на сфере Хаббла, удаляются от нас из-за расширения Вселенной со скоростью, равной скорости света. Заметим, что мы можем наблюдать галактики, находящиеся сейчас за сферой Хаббла. Следовательно, эта поверхность не является горизонтом.
Постоянная Хаббла меняется со временем (зато она одинакова во всех местах в данный момент времени). В нашей вселенной в течение всей ее истории по окончании стадии инфляции постоянная Хаббла уменьшается. Соответственно, поскольку скорость света постоянна, собственное расстояние до хаббловской сферы в настоящее время растет (т. е. в метрах, сантиметрах и т. д. это расстояние возрастает).
Вопрос в том, с какой скоростью увеличивается расстояние до сферы Хаббла. В ускоренно расширяющейся вселенной это расстояние растет со скоростью меньше световой, а в замедленно расширяющейся – быстрее. Точная формула для этой скорости c (1 + q), где q – так называемый параметр замедления; этот параметр меньше нуля во вселенной, расширяющейся с ускорением (у нас сейчас он равен примерно 0,55), и больше нуля – в противоположном случае. Знак параметра замедления обратен знаку второй производной масштабного фактора. Масштабный фактор в расширяющейся вселенной всегда растет, соответственно, его первая производная положительна. А вот вторая как раз отражает, происходит ли рост расстояний все быстрее и быстрее (ускоренно расширяющаяся вселенная) или нет.
В ускоренно расширяющейся вселенной галактики «вылетают» за сферу Хаббла, поскольку «чуть за» сферой Хаббла их скорость больше световой (вспомним, что не надо бояться сверхсветовых скоростей в космологии), и сфера от них отстает, потому что движется с меньшей скоростью. Это можно описать как «продвижение» сферы Хаббла в нашу сторону, если говорить о сопутствующем расстоянии. Таким образом, сопутствующее расстояние до сферы Хаббла уменьшается. Во Вселенной, расширяющейся с замедлением, ситуация обратная.
Замечу, что в космологии можно говорить о разных определениях расстояний, скоростей и времени. Если это не уточняется, то может возникать путаница. Подробнее почитать обо всем этом можно в серии статей на сайте «Астронет»
[95].
Приложение 2
Метод размерностей. Параметры в центре Солнца и пульсации звезд
Яркой иллюстрацией того, как с помощью качественных рассуждений можно получать правильные физические формулы, является метод размерностей
[96]. Мы рассмотрим здесь два простых примера: параметры в центре Солнца и период пульсаций звезд.