Напишите пример 3 +5 = 8
А на дне кружки «х». И, перевернув кружку, закройте цифру «5».
Что под кружкой?
Уверены, ребенок сразу угадает!
Теперь закройте цифру «5». Что под кружкой?

Так можно писать примеры на разные действия и играть. У ребенка происходит понимание, что х — это не просто непонятный знак, а «спрятанная цифра».
Шаг второй — научите определять, х в уравнении является целым или частью? Самым «большим» или «маленьким»?
Для этого нам подойдет техника «Яблоко».
Задайте ребенку вопрос, где в данном уравнении самое большое?
5 + х = 17.
Ребенок ответит: «17».
Отлично! Это будет наше яблоко!
Самое большое число — это всегда целое яблоко. Обведем в кружок.
А целое всегда состоит из частей. Давай подчеркнем части.
5 и х — части яблока.
А раз х — это часть. Она больше или меньше? х — большое или маленькое? Как его найти?
Важно отметить, что в таком случае ребенок думает и понимает, почему, чтобы найти х в данном примере, нужно из 17 вычесть 5.
После того как ребенок поймет, что ключом к правильному решению уравнений является определить х — целое или часть, он легко будет решать уравнения.
Потому что запомнить правило, когда понимаешь его, гораздо проще, чем наоборот: вызубрить и учиться применять.
Данные техники «Кружка» и «Яблоко» позволяют научить ребенка понимать, что он делает и зачем.
Три шага для родителей мальчиков:
— Используйте кружку для объяснения смысла уравнений.
— Играйте и закрывайте кружкой разные числа.
— Помогите ребенку понять уравнения, используя технику «Яблоко».
Техника №6. Математические лабиринты
Отлично работающий метод для закрепления навыка устного счета, который наверняка понравится деткам — математический лабиринт. Как с ним работать?
1. Попросите ребенка найти последовательно числа от 1 до 100. Если это первоклашка — то пусть это будут числа от 1 до 20.
2. Потом в обратную сторону двигаться с заданным шагом, например, -2.
3. Далее играем и меняем шаг счета: с шагом +2, -3, +5 и т. п. В прямую и обратную сторону.
Хард уровень — проделывать это с отвлечениями (читать стихи, петь песни и т. д.).
Такие тренировки не требуют много сил от детей, а если добавить замер времени и игровой момент, то являются очень эффективным тренажером для повышения скорости устного счета.
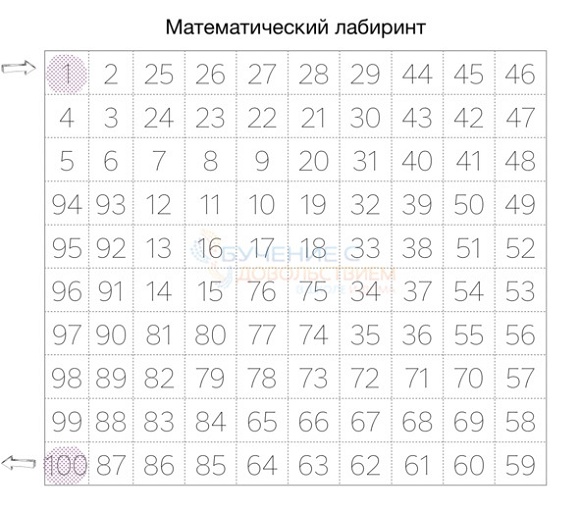
«Математический лабиринт»
Как с ним работать:
1. Попросите ребенка найти последовательно числа от 1 до 100. Если это первоклашка — то пусть это будут числа от 1 до 20.
2. Потом в обратную сторону двигаться с заданным шагом, например, -2.
3. Далее играем и меняем шаг счета: с шагом +2, -3, +5 и т. п. В прямую и обратную сторону.
Хард уровень — проделывать это с отвлечениями (читать стихи, петь песни и т.д.).
Такие тренировки не требуют много сил от детей, а если добавить замер времени и игровой момент, то являются очень эффективным тренажером для повышения скорости устного счета.
Можно играть в «Лабиринт» на время.
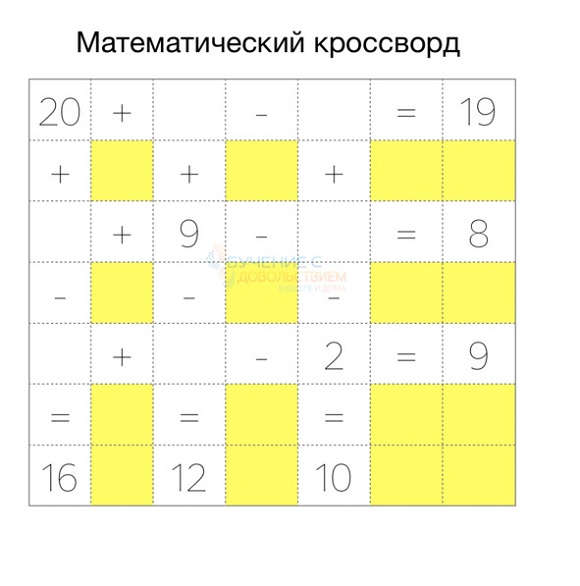
Техника №7. Математические кроссворды
В свое время стали находкой для моего младшего сына, который вообще никак не хотел учиться. Такие кроссворды вы можете составлять самостоятельно, ребенок может составлять их для вас, решать их можно устно и письменно.
Техника №8. «Камера хранения»
Данный метод позволяет изучить состав числа.
Представляет собой набор из 10 ячеек с точками внутри. Там видно, как различные комбинации чисел составляют счет в пределах 10. Прием «Камера хранения» особенно хорош в случае, когда надо показать, как работает вычитание.
У каждого из этих методов (метод пиктограмм, якорных слов и механического заучивания) есть свои плюсы и минусы.
Например, у механического метода плюс в том, что не надо возиться со всякими списками, пиктограммами, а нужно просто выучить наизусть. Но минус в том, что по сравнению с ассоциативными способами нагрузка на память довольно большая.
Меньшая нагрузка на память — это несомненный плюс метода пиктограмм, а с другой стороны, этот метод требует от нас некоторой изобретательности. Он поначалу непривычен, отнимает время и силы, но впоследствии мы к нему привыкаем.
Наверняка вы в магазинах видели камеры хранения — ячейки. Нарисовав камеру хранения на бумаге, вы можете положить в нее что-то или забрать. Останется посчитать, сколько ячеек свободно, а сколько занято.
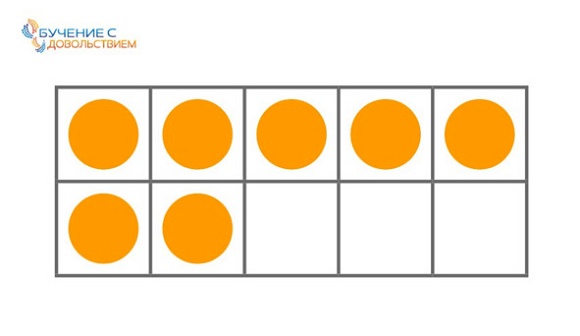
Метод «Камера хранения»
Техника №9. «Робот»
Робот держит какое-то количество предметов. При этом известно общее число и сколько в одной руке. Вам надо увидеть и сказать, сколько во второй.
На первом рисунке соотношение между цифрами 3 и 10 показано добавлением числа 7 в пустой круг (3 +7 = 10). Это помогает понять, как один номер можно разбить на более мелкие части. Во второй руке — семь. На втором рисунке: в первой руке — два.
В общем, суть метода такая: представьте, что само число — голова робота, а в руках он держит часть числа. Остается узнать, сколько во второй руке.
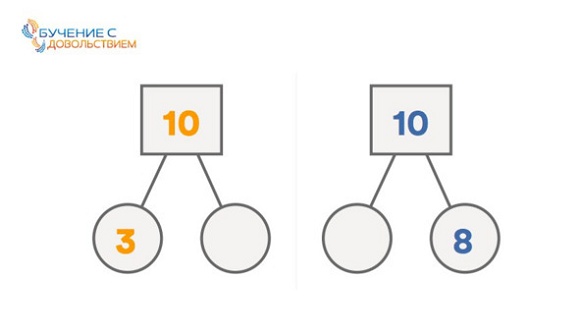
Метод «Робот»







