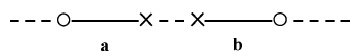6.233. На вопрос, нужна ли интуиция для решения математических задач, следует ответить: в этом случае интуицией служит язык.
6.2331. Процесс вычисления стимулирует интуицию.
Вычисление – не эксперимент.
6.234. Математика есть метод логики.
6.2341. Существенная черта математического метода – использование уравнений. Поскольку лишь при таком методе всякое математическое суждение понимается само по себе.
6.24. Метод, которым математика оперирует уравнениями, есть метод замещения. Ведь уравнения выражают взаимозаменяемость двух выражений, и, начиная с определенного числа уравнений, мы идем к новым уравнениям, заменяя различные выражения в соответствии с уравнениями.
6.241. Доказательство суждения 2 × 2 = 4 выглядит следующим образом:
(Ωv)υ, x = Ωv × υ, x Def.,
Ω2×2, x = (Ω2)2, x = (Ω2)1 + 1, x =
= Ω2, Ω2, x = Ω1 + 1, Ω1 + 1, x = (Ω’Ω)’(Ω’Ω)’x =
= Ω’Ω’Ω’Ω’x = Ω1 + 1 + 1 + 1, x = Ω4, x.
6.3. Изучение логики означает изучение всего, что подвластно ее законам. А вне логики все случайно.
6.31. Так называемый закон индукции не может быть законом логики, поскольку является осмысленным суждением. И невозможны априорные законы.
6.32. Закон причинности есть не закон, а форма закона.
6.321. «Закон причинности» – общее имя. И как в механике, к примеру, имеются «принципы минимума» – принцип наименьшего действия и т. д., – так и в физике имеются законы причинности, законы причинной формы.
6.3211. На самом деле люди предполагали, что должен быть некий «принцип наименьшего действия», прежде чем сумели его вывести. (Здесь, как и всегда, достоверное априори оказывается чисто логическим.)
6.33. У нас нет априорной веры в закон сохранения, зато есть априорное знание о возможности логической формы.
6.34. Все подобные суждения, включая принцип достаточного основания, закон непрерывности в природе и принцип наименьшего действия и т. д., суть априорные прозрения форм, в которых воплощаются суждения науки.
6.341. Ньютоновская механика, например, предусматривает общую форму описания мироздания. Допустим, есть белая плоскость с разбросанными по ней черными пятнами. Мы скажем, что каков бы ни был их узор, я всегда могу описать его максимально точно, наложив на поверхность мелкоячеистую сетку и приписав каждой ее квадратной ячейке значение черного или белого. Таким образом я введу обобщенную форму описания плоскости. Эта форма произвольна, поскольку того же результата я мог бы добиться, использовав сетку с треугольными или шестиугольными ячейками. Возможно, использование сетки с треугольными ячейками упростило бы описание: я хочу сказать, что, быть может, мы описали бы плоскость более аккуратно при помощи грубой треугольной сетки, а не мелкоячеистой квадратной (и наоборот). Различные сетки соответствуют различным системам описания мира. Механика определяет форму описания мира, утверждая, что все суждения, использованные в описании мира, должны быть созданы заданным способом из заданного набора суждений (аксиом механики). «Всякое здание, которое вы хотите возвести, каким бы оно ни было, должно быть построено из этих кирпичей, и только из них».
(Как с помощью системы счета записываются любые числа, так с помощью механики мы записываем любое физическое суждение, какое пожелаем.)
6.342. Теперь мы можем оценить сравнительное положение логики и механики. (Сетка может состоять из ячеек разных типов, то есть треугольные ячейки могут сочетаться с шестиугольными.) Возможность описания картины, подобной упомянутой выше, с сеткой заданной формы, ничего не рассказывает о самой картине. (Это верно для всех таких картин.) Картину характеризует то, что она может быть полностью описана при помощи конкретной сетки с ячейками конкретного размера.
Сходным образом сама возможность описания мира посредством ньютоновской механики ничего не говорит нам о мире; зато этот конкретный способ говорит, какими средствами возможно описать мир. Мы также узнаем кое-что о мире из того факта, что он может быть описан одной системой механики проще, чем другой.
6.343. Механика – попытка сконструировать согласно единому плану все истинные суждения, которые требуются для описания мира.
6.3431. Законы физики, со всем их логическим аппаратом, говорят, пусть не впрямую, об объектах мира.
6.3432. Не следует забывать, что любое описание мира посредством механики будет обобщенным. Например, механика не упоминает конкретные материальные точки, но только какие угодно точки.
6.35. Хотя пятна на нашей картине представляют собой геометрические фигуры, сама геометрия очевидно не говорит ничего об их реальной форме и расположении. Сеть, однако, полностью геометрична; все ее свойства могут быть заданы априорно.
Законы, подобные принципам достаточного основания, говорят о сети, а не о том, что сеть описывает.
6.36. Если существует закон причинности, он может быть выражен следующим образом: существуют законы природы.
Но, конечно, нельзя сказать: это проявляет себя.
6.361. Можно сказать, следуя Герцу: мыслимы лишь связи, подчиненные законам.
6.3611. Мы не можем сравнить процесс с «течением времени» – такого не существует, – но лишь с другим процессом (например, с работой хронометра). Так мы можем описать ход времени, лишь опираясь на другой процесс.
Нечто аналогичное применимо к пространству: когда говорят, что ни одно из двух событий не может произойти (одно исключает другое), ибо отсутствует причина, по которой одно должно наступить вероятнее другого, это значит, что мы не в состоянии описать одно из этих двух событий, пока не будет найдена некая асимметрия. А если такая асимметрия найдется, мы можем рассматривать ее как причину наступления одного и не-наступления другого события.
6.36111. Кантовская задача правой и левой рук11, которые не совпадают при наложении друг на друга, существует в плоскости.
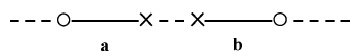
Она фактически существует в одномерном пространстве, в котором две конгруэнтные фигуры, a и b, не могут совпасть, пока их не выведут за пределы этого пространства. Правая и левая руки на деле полностью конгруэнтны, и не имеет значения, что они не могут быть сопряжены. Правую перчатку можно надеть на левую руку, если вывернуть ее наизнанку в четырехмерном пространстве.
6.362. Что может быть описано, может и произойти: то, что закон причинности призван исключить, произойти не может.