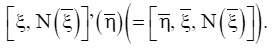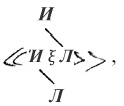6.002. Если дана общая форма, согласно которой строится суждение, тогда дана также и общая форма, согласно которой одно суждение порождается из другого посредством действия.
6.01. Поэтому общая форма действия «» такова:
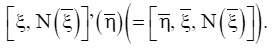
Это наиболее общая форма перехода от одного суждения к другому.
6.02. Здесь мы приходим к числам.
Я даю следующее определение:
x = Ω0, x Def., Ω’Ωv’x = Ωv + 1, x Def.
В соответствии с этими правилами сочетаний знаков мы записываем последовательность
x, Ω’x, Ω’Ω’x, Ω’Ω’Ω’x, …
в виде
Ω0, х, Ω0 + 1, x, Ω0 + 1 + 1, x, Ω0 + 1 + 1 + 1, x, ….
Поэтому вместо [x, ξ, Ω’ξ] я пишу
[Ω0, x, Ωv’x, Ωv + 1, x].
И даю следующие определения:
0 + 1 = 1 Def.,
0 + 1 + 1 = 2 Def.,
0 + 1 + 1 + 1 = 3 Def.
и т. д.
6.021. Число есть показатель действия.
6.022. Понятие числа подразумевает нечто общее для всех чисел, общую форму числа.
При этом понятие числа есть переменное число.
А понятие числового равенства есть общая форма всех частных случаев числового равенства.
6.03. Общая форма целого числа: [0, ξ, ξ + 1].
6.031. Теория классов в математике является совершенно излишней.
Это проистекает из того обстоятельства, что общность, которая обычно требуется в математике, не является случайной общностью.
6.1. Логические суждения суть тавтология.
6.11. Поэтому логические суждения не говорят ничего. (Они суть аналитические суждения.)
6.111. Все теории, наделяющие логическое суждение смыслом, ложны. Можно подумать, например, что слова «истинный» и «ложный» обозначают два свойства из множества, и тогда покажется удивительным, что всякое суждение всегда обладает одним из этих свойств. В рамках данной теории совершенно ясно, что, к примеру, суждение «Все розы либо красные, либо желтые» не самоочевидно, пусть даже оно истинно. На самом деле логические суждения приобретают все характеристики суждений естественных наук, а это верный признак того, что они построены неправильно.
6.112. Корректное истолкование логических суждений должно приписывать им уникальное положение среди всех суждений.
6.113. Особенность логического суждения в том, что можно понять его истинность только из символики, и этот факт содержит в себе всю философию логики. Очень важно также, что истинность или ложность не-логических суждений нельзя установить сугубо из них самих.
6.12. Тот факт, что логические суждения суть тавтология, показывает формальные – логические – свойства языка и мира.
То обстоятельство, что тавтология возникает посредством такого способа сочетания составных частей суждения, характеризует логику составных частей.
Если суждения порождают тавтологию, будучи соединены конкретным способом, они должны иметь определенные структурные свойства. Значит, возникновение тавтологии при специфическом сочетании суждений показывает, что они обладают структурными свойствами.
6.1201. Например, тот факт, что суждения «p» и «~p» в комбинации «(p × ~p)» дают тавтологию, показывает, что они противоречат друг другу. Факт, что суждения «p ⊃ q», «p» и «q» в комбинации «(p ⊃ q) × (p) : ⊃ : (q)» дают тавтологию, показывает, что q следует из p и p ⊃ q. Факт, что «(x) × fx : ⊃ : fa» есть тавтология, показывает: fa следует из (x) × fx, и т. д.
6.1202. Очевидно, что к подобному результату можно прийти, заменив тавтологию противоречием.
6.1203. Чтобы опознать в выражении тавтологию, в случаях когда не встречается знаков общности, можно прибегнуть к следующему интуитивному методу: вместо «p», «q», «r» и т. д. я записываю «ИpЛ», «ИqЛ», «ИrЛ» и т. п. Комбинации истинности я выражаю посредством скобок, например:
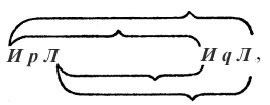
и я использую графические линии, чтобы выразить корреляцию истинности или ложности всего суждения с комбинациями истинности его истинностных аргументов следующим образом:
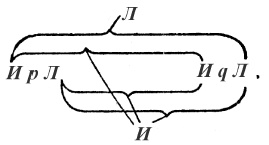
В итоге этот знак представляет выражение p ⊃ q. Далее, к примеру, я хочу изучить суждение ~(p × ~p) (закон противоречия), чтобы определить, является ли оно тавтологией. В нашей записи форма «~ξ» имеет вид
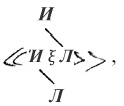
а форма «ξ × η» такова:
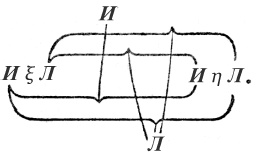
Поэтому предложение ~(p × ~q) записывается:
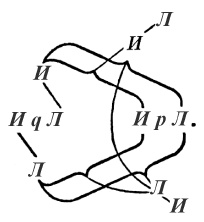
Если мы вставим «p» вместо «q» и рассмотрим, каким образом внешние И и Л соотносятся с внутренними, мы поймем, что истинность суждения в целом коррелирует со всеми комбинациями истинности его аргумента, а ложность не коррелирует ни с одной из таких комбинаций.
6.121. Логические суждения показывают логические свойства суждений, комбинируя последние так, что возникают суждения, которые не говорят ничего. Этот способ можно называть «нулевым методом».
В логическом суждении суждения приводятся в состояние равновесия по отношению друг к другу, и это состояние указывает, какой должна быть логическая конструкция этих суждений.
6.122. Отсюда следует, что мы вполне можем обойтись без логических суждений: ведь в корректной записи мы и без того можем определить формальные свойства суждений простой поверкой последних.
6.1221. Если, например, два суждения «p» и «q» в комбинации «p ⊃ q» дают тавтологию, тогда ясно, что q следует из p. К примеру, мы видим из этих суждений самих по себе, что «q» следует из «p ⊃ q × p», но также возможно показать это и следующим образом: мы объединяем суждения в форму «p ⊃ q × p : ⊃ : q» и затем показываем, что это тавтология.