Прецедент, к которому мы постоянно обращаемся, должен содержаться в самом символе.
5.526. Мы можем полностью описать мир посредством обобщенных суждений, без предварительного соотнесения имен с конкретными объектами.
Для последующего перехода к обычному способу выражения нужно к выражению «имеется один и только один х, который…» просто прибавить: «и этот х есть а».
5.5261. Обобщенное суждение, подобно любому другому суждению, является составным. (Это доказывается тем фактом, что в «(Ǝx, φ) × φx» нам приходится вводить «φ» и «x» раздельно. Оба индекса, независимо друг от друга, состоят в означающем отношении с миром, как и в случае необобщенных суждений.)
Это черта сложного символа, общая для него и для других символов.
5.5262. Истинность или ложность суждения оказывает влияние на общую конструкцию мира. А пространство, которое совокупность элементарных суждений предоставляет для его конструирования, соответствует тому, которое ограничено обобщенными суждениями.
(Если элементарное суждение истинно, это означает, что существует по крайней мере еще одно истинное элементарное суждение.)
5.53. Тождественность объектов я выражаю тождественностью знаков, а не использованием знака тождественности. Различие объектов я выражаю различием знаков.
5.5301. Очевидно, что тождественность не является отношением между объектами. Это становится ясно, если рассмотреть, к примеру, суждение «(x): fx. ⊃. x = a». Это суждение говорит о том, что лишь a удовлетворяет функции f, а не о том, что только предметы, имеющие какое-либо отношение к a, удовлетворяют этой функции.
Конечно, можно сказать, что только a имеет отношение к a; но чтобы выразить это, нам потребуется знак тождества.
5.5302. Расселовское определение «=» неудовлетворительно, поскольку согласно ему мы не можем сказать, что два объекта обладают полностью одинаковыми свойствами. (Даже если это суждение не является верным ни при каких условиях, оно все равно не лишено смысла.)
5.5303. Грубо говоря, сказать о двух предметах, что они тождественны, – бессмыслица; а сказать об одном предмете, что он тождественен себе, значит не сказать ничего.
5.531. Поэтому я записываю не «f (a, b) × a = b», но «f (a, a)» (или «f (b, b)»); и не «f (a, b) × ~a = b», но «f (a, b)».
5.532. Аналогично я записываю не «(Ǝx, y) × f (x, y) × x = y», но «(Ǝx) × f (x, x)»; и не «(Ǝx, y) × f (x, y) × ~x = y», но «(Ǝx, y) × f (x, y)».
(То есть вместо, как у Рассела, «(Ǝx, y) × f (x, y)» получаем «(Ǝx, y) × f (x, y) × ∨ × (Ǝx) × f (x, x)».)
5.5321. Потому, к примеру, вместо «(x): fx ⊃ x = a» мы пишем «(Ǝx) × fx × ⊃ × fa: ~ (Ǝx, y) × fx × fy».
А суждение «Только один x удовлетворяет f ()» будет записано как «(Ǝx) × fx: ~ (Ǝx, y) × fx × fy».
5.533. Знак равенства поэтому не является существенным элементом понятийной записи.
5.534. Теперь мы видим, что в корректной понятийной записи псевдосуждения вида «a = a», «a = b × b = c × ⊃ a = c», «(x) × x = x», «(Ǝx) × x = a» и т. д. не могут быть записаны вообще.
5.535. Это также устраняет трудности, связанные с подобными псевдосуждениями.
С помощью такого подхода можно разрешить все трудности, порожденные расселовской «аксиомой бесконечности».
То, что пытается сказать эта аксиома, будет выражено в языке посредством существования бесконечного количества имен с различными значениями.
5.5351. В некоторых случаях возникает искушение использовать выражения вида «a = a» или «p ⊃ p» и им подобные. На самом деле это происходит, когда затрагиваются прототипы, то есть суждения, предметы и т. д. В «Принципах математики» Рассела выражению «p есть суждение» – что бессмысленно – соответствует символическая запись «p ⊃ p», предпосланная в качестве гипотезы некоторым суждениям, чтобы заполнить их аргументные места только суждениями.
(Не имеет смысла помещать гипотезу «p ⊃ p» перед суждением, чтобы добиться правильности формы аргумента, хотя бы потому, что в случае не-суждения как аргумента эта гипотеза становится не просто ложной, но бессмысленной, и потому, что аргументы неправильной формы делают суждение бессмысленным; посему суждение предохраняет себя от аргументов неправильной формы столь же хорошо – или столь же плохо, – как добавленная к нему бессмысленная гипотеза.)
5.5352. Сходным образом стремятся выразить фразу «Предметы не существуют» записью «~(Ǝx) × x = x». Но даже будь это суждением, разве не оказалось бы оно истинным, если бы «предметы вправду существовали», но не были тождественны себе?
5.54. В общей пропозициональной форме суждения встречаются в других суждениях только как основы истинностных действий.
5.541. На первый взгляд похоже, будто для одного суждения возможно встречаться в другом отличным способом.
Особенно в ряде пропозициональных форм в психологии, например «A верит, что p имеет место» и «A думает, что p» и т. д.
Если рассуждать поверхностно, выглядит так, будто суждение p находится в некоем отношении к объекту A.
(В современной теории познания (Рассел, Мур10 и другие) подобные суждения конструируются именно таким образом.)
5.542. Ясно, однако, что «A верит, что p», «A думает, что p» и «A говорит p» имеют форму «“p” говорит p», и это не подразумевает соотнесения факта с объектом, а подразумевает, скорее, соотнесение фактов посредством соотнесения их объектов.
5.5421. Это показывает также, что нет такого феномена, как душа – субъект и т. п., – в том смысле, в каком она понимается в нынешней поверхностной психологии.
Ведь составная душа уже не будет душой.
5.5422. Корректное толкование пропозициональной формы «A делает умозаключение р» должно показать, что умозаключением не может не иметь смысла. (Теория Рассела не удовлетворяет этому требованию.)
5.5423. Чтобы постичь сложное, нужно постичь, что его части находятся в таких-то и таких-то отношениях друг с другом.
Это, вне сомнения, объясняет также, почему имеются два возможных способа восприятия куба и прочие подобные явления. Мы наблюдаем два различных факта.
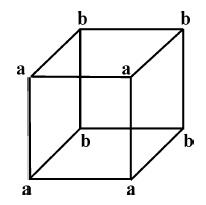
(Если я прежде всего смотрю на углы a и лишь потом на углы b, то углы a выступают вперед, и наоборот.)
5.55. Теперь мы должны априори ответить на вопрос относительно всех возможных форм элементарных суждений.



