LECAR, M., and FRANKLIN, F., “On the Original Distribution of the Asteroids.” Icarus, 20: 422–436 (1973).
MAROV, M. YA., “Venus: A Perspective at the Beginning of Planetary Exploration.” Icarus, 16: 415–461 (1972).
MAROV, M. YA., AVDUEVSKY, V., BORODIN, N., EKONOMOV, A., KERZHANOVICH, V., LYSOV, V., MOSHKIN, B., ROZHDESTVENSKY, M., and RYABOV, O., “Preliminary
Results on the Venus Atmosphere from the Venera 8 Descent Module.” Icarus, 20: 407–421 (1973).
MEEUS, J., “Comments on The Jupiter Effect.” Icarus, 26: 257–267 (1975).
NEUGEBAUER, O., “Ancient Mathematics and Astronomy,” in The History of Technology, edited by C. Singer, E. J. Holmyard, and Hall, A. R. London, Oxford University Press, 1954.
ÖPIK, ERNST J., “Collision Probabilities with the Planets and the Distribution of Interplanetary Matter.” Proceedings of the Royal Irish Academy, Vol. 54 (1951), 165–199.
OWEN, T. C., and SAGAN, C., “Minor Constituents in Planetary Atmospheres: Ultraviolet Spectroscopy from the Orbiting Astronomical Observatory.” Icarus, 16: 557–568 (1972).
POLLACK, J. B., “A Nongray CO2-H20 Greenhouse Model of Venus.” Icarus, 10: 314–341 (1969).
POLLACK, J. B., ERICKSON, E., WITTEBORN, F., CHACKERIAN, C., SUMMERS, A., AUGASON, O., and CAROFF, L., “Aircraft Observation of Venus’ Near-infrared Reflection Spectrum: Implications for Cloud Composition.” Icarus, 23: 8–26 (1974).
SAGAN, C., “The Radiation Balance of Venus.” California Institute of Technology, Jet Propulsion Laboratory, Technical Report 32–34, 1960.
–, “The Planet Venus. “ Science, 133: 849 (1961).
–, The Cosmic Connection. New York, Doubleday, 1973.
–, “Erosion of the Rocks of Venus.” Nature, 261:31 (1976).
SAGAN, C., and PAGE T., eds., UFOs: A Scientific Debate. Ithaca, N. Y., Cornell University Press, 1973; New York, Norton, 1974.
SILL, G.,·”Sulfuric Acid in the Venus Clouds.” Communications Lunar Planet Lab., University of Arizona, 9: 191–198 (1972).
SPITZER, LYMAN, and BAADE, WALTER, “Stellar Populations and Collisions of Galaxies.” Ap. J., 113: 413 (1951).
UREY, H. C., “Cometary Collisions and Geological Periods.” Nature, 242: 32–33 (1973).
–, The Planets, New Haven, Yale University Press, 1951.
VELIKOVSKY, I., Worlds in Collision. New York, Dell, 1965. (First printing, Doubleday, 1950.)
–, “Venus, a Youthful Planet.” Yale Scientific Magazine, 41: 8–11 (1967).
VITALIANO, DOROTHY B., Legends of the Earth: Their Geologic Origins. Bloomington, Indiana University Press, 1973.
WILDT, R., “Note on the Surface Temperature of Venus.” Ap. J., 91: 266 (1940).
–, “On the Chemistry of the Atmosphere of Venus.” Ap. J., 96: 312–314 (1942).
YOUNG, A. T., “Are the Clouds of Venus Sulfuric Acid?” Icarus, 18: 564–582 (1973).
YOUNG, L. D. G., and YOUNG, A. T., Comments on “The Composition of the Venus Cloud Tops in Light of Recent Spectroscopic Data.” Ap. J., 179: L39 (1973).
Приложения к главе 7
Приложение 1
Простое обсуждение физических аспектов вероятности недавнего столкновения с Землей массивного члена Солнечной системы
Здесь мы рассматриваем вероятность того, что массивный объект такого типа, который имеет в виду Великовский, отделился от Юпитера и столкнулся с Землей. Великовский предполагает, что эта комета прошла по касательной рядом с Землей. Для простоты назовем эту идею столкновением. Рассмотрим сферический объект радиусом R, движущийся среди других объектов подобного размера. Столкновение произойдет, когда центры объектов окажутся на расстоянии 2R. В таком случае мы можем говорить об эффективном поперечном сечении столкновения σ = π (2R)2 = 4πR2; это площадь мишени, в которую должен удариться центр движущегося объекта, чтобы произошло столкновение. Давайте предположим, что только один такой объект (комета Великовского) движется, а остальные (планеты внутренней Солнечной системы) неподвижны. Это пренебрежение движением планет внутренней Солнечной системы может вызвать погрешность меньше, чем в два раза. Пусть комета будет двигаться со скоростью v, а пространственная плотность потенциальных мишеней (планет внутренней Солнечной системы) будет n. Мы будем использовать следующие единицы измерения: R – в сантиметрах (см), σ – в см2, v – в см/с и n – в количестве планет в 1 см3. Очевидно, что n – очень малое число.
Хотя у комет широкий диапазон углов наклонения орбит к плоскости эклиптики, ради гипотезы Великовского мы сделаем самое щедрое допущение, если примем самое малое возможное значение этого наклона. Если бы не было ограничений по наклонению орбиты кометы, она бы с одинаковой вероятностью двигалась бы повсюду в области пространства с Солнцем в центре и радиусом r = 5 астрономических единиц (1 а.е. = 1,5 × 1013 см), большой полуоси орбиты Юпитера. Чем больше пространство, в котором может перемещаться комета, тем меньше вероятность ее столкновения с другим объектом. Вследствие быстрого вращения Юпитера любой объект, вылетевший из него, будет двигаться в экваториальной плоскости планеты, угол наклона которой к плоскости вращения Земли вокруг Солнца составляет 1,2°. Однако, чтобы комета вообще достигла внутренней части Солнечной системы, ее отделение от планеты должно быть достаточно энергичным, так что возможно практически любое значение наклонения ее орбиты i. Самое низкое значение в таком случае – i = 1,2°. Следовательно, мы рассматриваем комету, которая движется (см. диаграмму) по орбите, проходящей где-то в клинообразном пространстве с центром в области Солнца (одним фокусом орбиты кометы должно быть Солнце) и с полууглом наклона, равным i. Ее объем тогда составляет: (4/3) πr3 sin i = 4 × 1040 см3, то есть только 2 % от полного объема сферы радиусом r. Поскольку в этом пространстве находится (не считая астероидов) три или четыре планеты, пространственная плотность мишеней, относящихся к нашей проблеме, составляет около 10–40 планет/см3. Типичная относительная скорость кометы или другого объекта, движущегося по эксцентричной орбите во внутренней Солнечной системе, может составлять около 20 км/с. Радиус Земли R = 6,3 × 108 см, что почти точно равно радиусу планеты Венера.
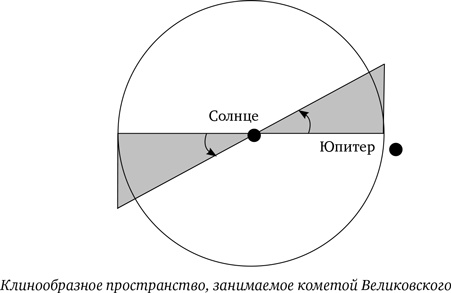
Сейчас давайте представим, что эллиптический путь кометы выпрямлен и что она движется какое-то время Т, пока не столкнется с планетой. В течение этого времени она проложит за собой воображаемый туннель объемом σvT см³, и в этом пространстве должна поместиться только одна планета. Но 1/n – также объем, вмещающий одну планету. Следовательно, две величины равны и справедливо равенство

