Механику реактивного движения описывают с помощью третьего закона Ньютона. Мы со школы помним его формулировку: тела действуют друг на друга силами, равными по модулю и противоположными по направлению. Или: сила противодействия равна силе действия. В случае ракет силой действия является тяга, которая создается раскаленными газами, вырывающимися из сопла. Они и толкают ракету в противоположную сторону. Поэтому ракета не нуждается в приложении каких-то других сил; она сама создает силу действия, а за счет силы противодействия, реакции, отдачи летит с ускорением не только в атмосфере, но и в космосе.

«Союз-ФГ» стартует с космодрома Байконур 28 июля 2017 года (фотография Андрея Шелепина /ЦПК)

В то же время реактивным называют и движение, при котором для создания сил действия и противодействия используется окружающая среда. Например, турбореактивный двигатель авиалайнера использует окружающий воздух для создания рабочей газовой смеси. Кальмар прокачивает через свое тело окружающую воду для разгона при охоте или бегстве. Но, конечно, ни авиалайнер, ни кальмар не смогут летать в космосе.
Какая скорость нужна, чтобы выйти на орбиту?
Очень большая. Но развивать ее можно постепенно, как и делает ракета, поднимаясь на космическую высоту. С какого-то момента скорость становится такой, что ракета выйдет на орбиту. Мысленный эксперимент поставил еще великий Исаак Ньютон. Представьте себе высочайшую гору, пик которой находится за пределами атмосферы. Вообразите пушку, установленную на самой ее вершине и стреляющую горизонтально. Чем мощнее заряд используется при выстреле, тем дальше от горы будет улетать ядро. Наконец при достижении некоторой мощности заряда ядро разовьет такую скорость, что не упадет на Землю вообще и будет вращаться вокруг нашей планеты. Фактически Ньютон описал искусственный спутник, а значение вычисленной им начальной скорости – 7,91 км/с. Ее сегодня называют «первой космической».
Если говорить с физической точки зрения, то спутник на самом деле всё время падает под действием силы притяжения, но не может упасть, потому что земная поверхность как бы «убегает» от него за счет собственной кривизны. Вот если бы Земля была плоская, то спутники неизбежно падали бы на нее, пролетев какое-то расстояние. И понятно, что если бы движение спутника происходило не в вакууме, а в атмосфере, то он тоже упал бы, потому что молекулы воздуха при бесчисленных столкновениях затормозили бы его.
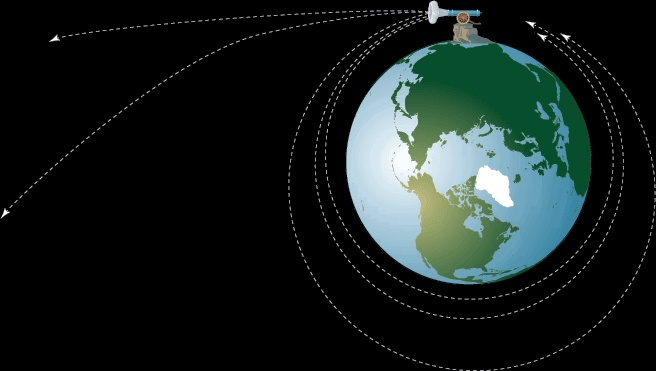
Пушка Ньютона
С удалением от Земли величина первой космической скорости снижается, ведь и сила притяжения уменьшается. Например, на высоте 100 км скорость равна 7,85 км/с, а на высоте полета Международной космической станции – 7,67 км/с. Немного изменяя скорость спутника, можно сделать его орбиту эллиптической, а путем довольно хитрых маневров – вывести на такую высоту, где его угловая скорость относительно планеты станет равна скорости ее вращения, в результате получится, что спутник как бы висит над одной точкой земного шара, хотя в действительности он продолжает падать.
Какая скорость нужна, чтобы добраться до Луны и Марса?
Чтобы космический аппарат вышел в межпланетное пространство на собственную орбиту вокруг Солнца, ему нужно развить скорость, которую называют «второй космической», или «скоростью убегания»; для нашей планеты она составляет 11,19 км/с. Ее значение тоже меняется с высотой, поэтому специалисты обычно используют значение 11,02 км/с, которое соответствует высоте 200 км – именно там проходит «промежуточная» орбита, с которой стартуют межпланетные аппараты. Но Луна находится поблизости от нас в общей гравитационной системе, поэтому для того, чтобы попасть в спутник Земли по прямой траектории, нет необходимости развивать «скорость убегания»: для старта с земной поверхности достаточно разогнаться до 11,09 км/с, а с «промежуточной» орбиты – до 10,92 км/с. Правда, лететь тогда придется дней пять.
При полете к Марсу ситуация усложняется. В межпланетном пространстве влияние гравитации Земли настолько мало, что им пренебрегают. Поэтому имеет смысл говорить только о скорости относительно Солнца. Минимальная «скорость убегания» от Солнца – 42,12 км/с – в четыре раза больше, чем от Земли! Но если мы стартуем в направлении по движению нашей планеты вокруг Солнца, то используем ее собственную скорость, которая близка к 29,78 км/с. Значит, необходимо иметь «на бесконечности», где притяжение Земли уже пренебрежимо мало, скорость 12,34 км/с. Это соответствует скорости отлета с низкой орбиты примерно 16,54 км/с относительно Земли – ее называют «третьей космической» скоростью. Рассчитать ее можно через закон сохранения энергии.
К счастью, для полета к Марсу такой большой скорости не нужно. Давным-давно рассчитаны траектории межпланетных полетов, которые требуют минимум топлива. Их называют траекториями – Гомана в честь немецкого инженера Вальтера Гомана, который вычислил их одним из первых. Чтобы выйти на траекторию полета к Марсу с минимальными затратами топлива, нужно разогнать космический аппарат до скорости 11,42 км/с – ненамного больше, чем для полета на Луну. Однако Марс при этом должен находиться в благоприятном положении относительно Земли, которое устанавливается раз в два года с небольшим – точнее, через 780 суток. Период, когда возможен полет к Марсу по гомановской траектории, называют «стартовым окном». Сам полет, если сделать всё правильно, будет продолжаться 259 дней. Можно сократить время перелета, чуть увеличив начальную скорость. Например, если скорость поднять до 11,8 км/с, то аппарат доберется до Марса за 165 дней; если до 12 км/с, то за 144 дня; если до 13 км/с, то за 105 дней.
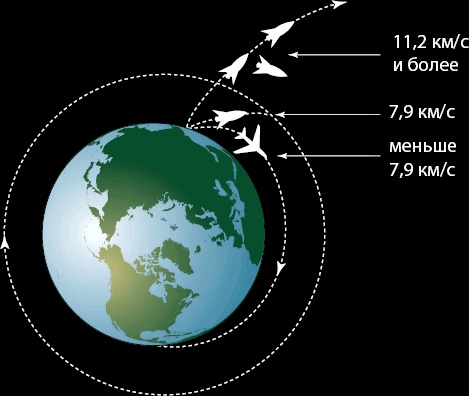
Космические скорости
Конечно, теоретически по Солнечной системе можно летать по каким угодно траекториям, но у нас пока нет настолько мощных кораблей, чтобы нарушать законы баллистики, а когда они появятся, сказать трудно.
Почему Земля не плоская?
Если вы смотрели документальные фильмы о космосе, то, наверное, заметили, что капли воды в невесомости становятся шарообразными. Но почему? Форма предметов меняется только под действием какой-то силы. Что за сила действует на воду? Это, конечно, сила поверхностного натяжения. Под ее действием жидкость стремится принять форму с минимальной площадью поверхности, а лучшая форма для этого – шар.

