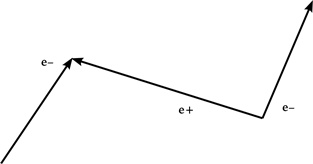
Если вас это не взволновало, задумайтесь вот над чем: ситуация начинается с одной частицы и заканчивается одной частицей, но где-то в промежутке некоторое время существует три движущиеся частицы.
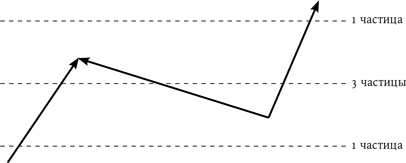
Где-то в середине процесса, пусть совсем недолго, но все же существует нечто, порожденное из ничего!
В своей статье 1949 г. «Теория позитронов» Фейнман приводит прекрасную аналогию из реальности военного времени:
Здесь дело обстоит так же, как в том случае, когда летящий низко над дорогой пилот видит некоторое время вместо одной дороги три, хотя на самом деле имеется только двойной поворот одной и той же дороги
[17].
Если время, за которое происходят эти «американские горки», достаточно мало и мы не можем измерить параметры частиц непосредственно, квантовая механика и теория относительности не просто допускают такое дикое положение дел – они его требуют. Частицы, появляющиеся и исчезающие за такие короткие промежутки времени, что их невозможно измерить, называются виртуальными.
Разумеется, рассуждения о совершенно новом наборе частиц в пустом пространстве, которые еще и невозможно зарегистрировать, выглядят примерно как предположение, что на кончике иглы танцует великое множество ангелов. И идея эта была бы настолько же бесплодной, если бы эти частицы не порождали никаких других измеримых эффектов. Но, хотя прямо такие частицы пронаблюдать невозможно, оказывается, что их косвенное воздействие обеспечивает большинство характеристик Вселенной, которую мы сейчас наблюдаем. Мало того, действие этих частиц может быть рассчитано с большей точностью, чем получается при любом другом вычислении в науке!
Рассмотрим, к примеру, атом водорода – систему, ради объяснения которой Бор разрабатывал квантовую теорию, а Шрёдингер выводил свое знаменитое уравнение. Красота квантовой механики состоит в том, что она могла объяснить возникновение специфических цветов света, который водород излучает при нагреве, на основании того, что электроны, вращающиеся вокруг протона, могут существовать только на дискретных энергетических уровнях, а когда они перескакивают с уровня на уровень, то поглощают или испускают лишь фиксированный набор световых частот. Уравнение Шрёдингера позволяет вычислить эти частоты и получить почти в точности верный ответ.
Почти, но не в точности.
Когда спектр водорода исследовали более тщательно, оказалось, что он сложнее, чем считалось ранее, и между наблюдаемыми уровнями есть еще дополнительные мелкие расщепления, это называется тонкой структурой спектра. Эти расщепления были известны еще со времен Бора, существовало подозрение, что они имеют какое-то отношение к релятивистским эффектам, но это подозрение никто не мог подкрепить, пока ученые не получили в свое распоряжение полностью релятивистскую теорию. К счастью, уравнение Дирака дало более точные результаты, чем уравнение Шрёдингера, и позволило воспроизвести общую картину наблюдений, в том числе и тонкую структуру.
Казалось, все в порядке, но вот в апреле 1947 г. американский физик-экспериментатор Уиллис Лэмб и его студент Роберт Резерфорд провели эксперимент, который в других обстоятельствах мог бы показаться на удивление ненужным и неоправданным. Исследователи поняли, что у них хватает технических средств, чтобы измерить структуру энергетических уровней атомов водорода с точностью до одной стомиллионной. Почему они вообще решили этим заняться? Дело в том, что, когда экспериментаторы находят новый метод нечто измерить с точностью, значительно превосходящей прежние возможности, для них это зачастую становится вполне достаточным стимулом приниматься за работу. В результате таких экспериментов удавалось открыть буквально новые миры – например, когда в 1676 г. голландский ученый Антони Филипс ван Левенгук решил рассмотреть под микроскопом капельку якобы чистой воды и обнаружил, что в ней кишит жизнь. Однако в нашем случае у экспериментов была более практическая цель. До эксперимента Лэмба было невозможно достичь такой точности, чтобы подробно проверить предсказания Дирака.
Уравнение Дирака позволяло предсказать общую структуру новых наблюдений, но главный вопрос, на который хотел ответить Лэмб: предсказывает ли оно все детали? Это был единственный способ проверить теорию. И когда Лэмб проделал свой эксперимент, получилось, что теория Дирака дает неверный ответ на уровне примерно 100 частей на миллиард, что значительно превышало чувствительность его установки.
Казалось бы, погрешность минимальная, однако и предсказания самой простой интерпретации теории Дирака, и эксперимент не допускали двояких толкований – и при этом они не соответствовали друг другу.
В течение нескольких следующих лет лучшие умы теоретической физики подключились к делу и попытались разрешить это несоответствие. Решение пришло лишь после долгого и упорного труда, и в сухом остатке оказалось, что уравнение Дирака дает исключительно точный ответ, но только если учесть воздействие виртуальных частиц. Это можно наглядно проиллюстрировать следующим образом. В учебниках по химии атомы водорода принято изображать примерно так: в серединке протон, вокруг по орбите вращается электрон, перескакивая на разные уровни:
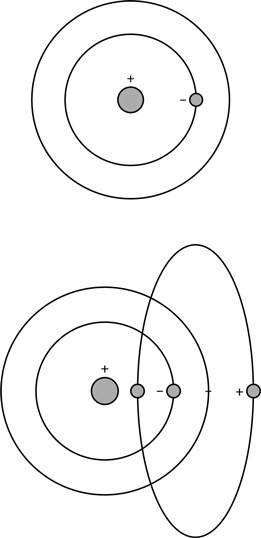
Однако стоит нам допустить возможность того, что пары «электрон-позитрон» способны на миг возникать из ничего, а потом аннигилировать, то пройдет совсем немного времени и атом водорода будет выглядеть вот так:
Справа я изобразил подобную пару, которая потом аннигилирует. Виртуальный электрон, будучи отрицательно заряжен, предпочитает держаться поближе к протону, а позитрон – отстраняться. Так или иначе из рисунка ясно, что подлинное распределение зарядов в атоме водорода ни в какой момент времени нельзя описывать как просто протон и один-единственный электрон.
Примечательно, что мы, физики, выяснили (после долгих и упорных трудов Фейнмана и его коллег), что можно использовать уравнение Дирака для вычисления влияния на спектр водорода всех возможных виртуальных частиц, способных мелькать в его окрестностях с какой угодно точностью. И при этом у нас получается самое лучшее, самое точное предсказание во всей науке. Рядом с ним меркнут все другие научные прогнозы. В астрономии самые свежие данные наблюдений реликтового излучения можно сравнить с теоретическими предсказаниями с точностью, скажем, в одну стотысячную, и это внушает уважение. Однако уравнение Дирака – с учетом предсказанного существования виртуальных частиц – позволяет рассчитывать параметры атома, которые будут совпадать с данными наблюдений на уровне одной миллиардной и даже лучше!





