И наконец, нужно обратить внимание на то, что, хотя мы здесь и абстрагируем термины трудности от чисел, для того чтобы исследовать ее природу, но она, однако, часто оказывается легче разрешимой с помощью данных чисел, чем без них. Это происходит при двойном применении чисел, ибо, как мы видели выше, именно одни и те же числа объясняют то порядок, то меру. Поэтому, после того как мы пытались разрешить трудность, выразив ее в общих терминах, нужно снова свести ее на эти числа, для того чтобы узнать, не могут ли они дать нам более простого решения. Например, найдя, что основание прямоугольного треугольника с катетами а и b равно
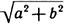 , где вместо а² нужно взять 81 и вместо b² — 144, числа, дающие в сумме число 225, корень которого (т. е. средняя пропорциональная между единицей и 225) равен 15, мы из этого узнаем, что основание 15 соизмеримо со сторонами 9 и 12, но не потому вообще, что оно является основанием такого треугольника, отношение сторон которого равно 3 к 4. Все это мы различаем потому, что стремимся достичь очевидного и отчетливого познания вещей, счетчики же не делают этого потому, что удовлетворяются отысканием нужного им числа, не замечая зависимости его от данных чисел, между тем как только в этом и заключается наука.
, где вместо а² нужно взять 81 и вместо b² — 144, числа, дающие в сумме число 225, корень которого (т. е. средняя пропорциональная между единицей и 225) равен 15, мы из этого узнаем, что основание 15 соизмеримо со сторонами 9 и 12, но не потому вообще, что оно является основанием такого треугольника, отношение сторон которого равно 3 к 4. Все это мы различаем потому, что стремимся достичь очевидного и отчетливого познания вещей, счетчики же не делают этого потому, что удовлетворяются отысканием нужного им числа, не замечая зависимости его от данных чисел, между тем как только в этом и заключается наука.
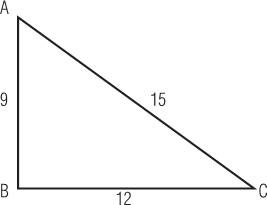
Заметим теперь вообще, что не нужно вверять памяти вещи, не требующие нашего постоянного внимания, если мы можем закреплять их на бумаге, во избежание того, чтобы бесполезный труд их припоминания не отвлекал наше мышление от того объекта, которым оно занято в данный момент. Кроме того, нужно составить таблицу, чтобы внести в нее сначала условия задачи в том виде, как они представляются с первого взгляда, затем — способ их абстрагирования и фигуры, посредством которых они обозначаются, чтобы, после того как мы найдем решение в самих знаках, мы могли легко и без всякого участия памяти применить его к частному предмету, с которым мы будем иметь дело. Нельзя именно абстрагировать какую-либо вещь иначе, нежели от какой-либо другой, менее общей. Это я запишу, следовательно, так: в прямоугольном треугольнике АВС нужно найти основание АС. Затем я отвлекаюсь от особенностей задачи, для того чтобы найти вообще величину основания по величине сторон; затем вместо стороны АВ, которая равна 9, я беру а, вместо стороны ВС, которая равна 12, я беру b, и т. д.
Нужно заметить, что мы будем пользоваться этими четырьмя правилами в третьей части настоящего трактата, где дадим им несколько более широкое применение, нежели это было объяснено здесь, как будет показано в своем месте.
Математика для Декарта не сводится к арифметическому исчислению, но также выражает и пропорции. Это означает, что математически выражается не только величина, но и порядок, который можно представить и наглядно геометрически, и абстрактно в краткой алгебраической форме. В свою очередь, алгебраическая форма выражения мысли позволяет находить решения задач, не перегружая память лишней информацией.
Правило XVII
Встретившуюся трудность нужно просматривать прямо, не обращая внимания на то, что некоторые из ее терминов известны, а некоторые неизвестны, и интуитивно следовать правильным путем по их взаимной зависимости
Это правило предписывает рассматривать проблему в целостности, выявляя взаимосвязь между всеми элементами, независимо от того, известны они нам или нет. Их все знать невозможно, но это не препятствует ученому смотреть на явления природы с позиции целостности.
Четыре предшествующих правила учили, как нужно абстрагировать от отдельных предметов определенные и в совершенстве осмысленные трудности и сводить их к тому, чтобы после этого нам оставалось отыскивать именно только величины по тем или иным отношениям, связующим их с данными величинами. В следующих же пяти правилах мы объясним, как нужно решать эти трудности, чтобы независимо от количества неизвестных величин, содержащихся в одном положении, эти величины пришли к взаимному подчинению, и тем, чем является первая величина по отношению к единице, вторая была бы по отношению к первой, третья — по отношению ко второй, четвертая — по отношению к третьей, чтобы они, следуя таким же образом далее, независимо от их количества, в целом составили сумму, равную именно данной величине. Все это должно производиться путем столь строгого метода, чтобы с помощью его мы твердо убедились в невозможности приведения этих величин к более простым терминам никакими способами.
Что же касается настоящего правила, то заметим, что во всяком вопросе, подлежащем разрешению именно дедуктивным путем, есть один открытый и прямой путь, по которому мы можем легче всего переходить от одного термина к другому, тогда как все другие пути являются более трудными и косвенными. Для того чтобы это понять, нам нужно вспомнить сказанное нами в правиле XI, где, объясняя сцепление положений, мы указали, что если сравнивать каждое положение с его предшествующим и последующим, то можно без труда заметить, что первое и последнее из них связываются друг с другом, хотя мы и не можем с такой же легкостью выводить промежуточные положения из крайних. Следовательно, теперь, если мы рассматриваем их взаимную зависимость, нигде не прерывая порядка, чтобы сделать из этого вывод, в какой зависимости находится последнее положение от первого, такое рассмотрение будет прямым. Если же, наоборот, зная, что первое и последнее находятся между собой в некоторой связи, мы пожелаем сделать вывод, каковы промежуточные, соединяющие их положения, то мы будем идти косвенным и превратным для порядка путем. Поскольку же нас интересуют здесь только неясные вопросы, в которых нужно именно при известных крайних найти без твердого порядка промежуточные, все искусство здесь должно состоять в том, чтобы, предполагая известным неизвестное, находить себе таким образом легкий и прямой путь также и для разрешения самых трудных вопросов. И нет ничего, что могло бы препятствовать неизменному успеху подобного действия, поскольку мы предположили в начале этой части, что нам известна такая зависимость неизвестного в данном вопросе от известного, которая совершенно определяет первое последним. Таким образом, если мы размышляем о тех самых вещах, которые представляются нам прежде всего, после того как мы примем это определение, то, хотя бы мы по неведению причисляли их к известным, для того чтобы постепенно выводить из них все остальные, а также и известные правильным путем так, как если бы они были неизвестными, мы исполняем все предписания этого правила. Что касается примеров того, что мы хотим здесь объяснить, а также и многих других вещей, о которых мы должны говорить в дальнейшем, то мы отложим их до правила XXIV, ибо там они будут более уместны.
Не только Декарт, но и другие представители самых различных наук используют метод познания неизвестного путем выявления его взаимосвязи с другими явлениями с позиции целостного восприятия явления. Самое простое алгебраическое выражение этого метода — уравнение. Мы просто записываем неизвестную величину наряду с известными так, чтобы путем преобразований найти, в конечном счете, неизвестное значение.



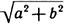 , где вместо а² нужно взять 81 и вместо b² — 144, числа, дающие в сумме число 225, корень которого (т. е. средняя пропорциональная между единицей и 225) равен 15, мы из этого узнаем, что основание 15 соизмеримо со сторонами 9 и 12, но не потому вообще, что оно является основанием такого треугольника, отношение сторон которого равно 3 к 4. Все это мы различаем потому, что стремимся достичь очевидного и отчетливого познания вещей, счетчики же не делают этого потому, что удовлетворяются отысканием нужного им числа, не замечая зависимости его от данных чисел, между тем как только в этом и заключается наука.
, где вместо а² нужно взять 81 и вместо b² — 144, числа, дающие в сумме число 225, корень которого (т. е. средняя пропорциональная между единицей и 225) равен 15, мы из этого узнаем, что основание 15 соизмеримо со сторонами 9 и 12, но не потому вообще, что оно является основанием такого треугольника, отношение сторон которого равно 3 к 4. Все это мы различаем потому, что стремимся достичь очевидного и отчетливого познания вещей, счетчики же не делают этого потому, что удовлетворяются отысканием нужного им числа, не замечая зависимости его от данных чисел, между тем как только в этом и заключается наука.