
Онлайн книга «Вселенная Стивена Хокинга»
Именно на конференции в Ватикане, уже упомянутой, я впервые высказал предположение, что, возможно, пространство и время совместно образовали поверхность, конечную по размеру и притом безграничную. Правда, моя статья носила скорее математический характер, и поэтому ее следствия о роли Бога в сотворении космоса тогда не были осознаны большинством (да и мной самим). Ко времени ватиканского мероприятия я еще не знал, как воспользоваться безграничностью для предсказаний о Вселенной.
Следующее лето я провел в Калифорнийском университете в Санта-Барбаре. Там с моим другом и коллегой Джеймсом Хартлом мы установили, каким условиям должна удовлетворять Вселенная, чтобы пространство-время не имело границ. По возвращении в Кембридж я продолжил работу с двумя своими аспирантами, Джулианом Латтрелом и Джонатаном Хэлливеллом.
Идея о том – и это важно отметить, – что пространство и время конечны, но при этом не имеют границ, есть гипотеза: ее нельзя вывести из какого бы то ни было другого принципа. Как и любую другую научную теорию, ее можно выдвинуть из чисто эстетических или метафизических соображений, но подлинной проверкой являются предсказания на ее основе, которые согласуются с наблюдениями. В случае квантовой теории гравитации это, однако, трудно обеспечить по двум причинам. Во-первых, как станет понятно из главы 11, мы пока не уверены, какая из теорий успешнее других сочетает общую теорию относительности и квантовую механику, хотя уже много знаем о том, какую форму эта теория должна иметь. Во-вторых, любая модель, в подробностях описывающая целую Вселенную, будет математически слишком сложной, чтобы с ее помощью получить точные предсказания. Поэтому приходится делать упрощающие предположения и использовать приближения, хотя и в этом случае получение предсказаний остается чрезвычайно трудной задачей.
Каждая траектория в фейнмановском методе описывает не только пространство-время, но и все, что в нем находится, включая сложные организмы – например людей, – которые могут наблюдать историю Вселенной. Это дает нам дополнительный аргумент в пользу антропного принципа: если все траектории (истории) возможны, то, раз мы существуем внутри одной из траекторий (историй), мы можем применить антропный принцип, чтобы объяснить, почему Вселенная такова, какова она есть. О смысле других историй, или траекторий, в которых нас нет, сложно судить однозначно. Однако этот взгляд на квантовую теорию гравитации был бы куда более приемлемым, если бы удалось показать, что наша Вселенная – не просто одна из многих возможных траекторий, но и одна из наиболее вероятных. Для этого надо выполнить суммирование по траекториям всех возможных евклидовых разновидностей пространства-времени, не имеющих границ.
В рамках «безграничной» гипотезы ничтожно мала вероятность того, что Вселенная эволюционирует согласно большинству из возможных траекторий, но при этом имеется семейство траекторий, более вероятных, чем остальные. Их можно изобразить при помощи поверхности Земли: расстояние от Северного полюса представляет мнимое время, а размер окружности, все точки которой находятся на постоянном расстоянии от Северного полюса, – пространственный размер Вселенной. Вселенная начинается на Северном полюсе в виде мельчайшей точки. По мере продвижения на юг дуги параллелей на постоянном расстоянии от Северного полюса увеличиваются, что соответствует расширению Вселенной с течением мнимого временем (рис. 8.1). Вселенная достигает максимального размера на экваторе, после чего начинает сжиматься, по мере того как прирастает мнимое время, пока наконец не схлопнется до размеров точки на Южном полюсе. И хотя на Северном и Южном полюсах диаметр Вселенной равен нулю, эти точки не будут сингулярностями, точнее, они будут не более сингулярны, чем Северный и Южный полюса Земли. Законы физики там должны соблюдаться так же, как на противоположных концах планетной оси.
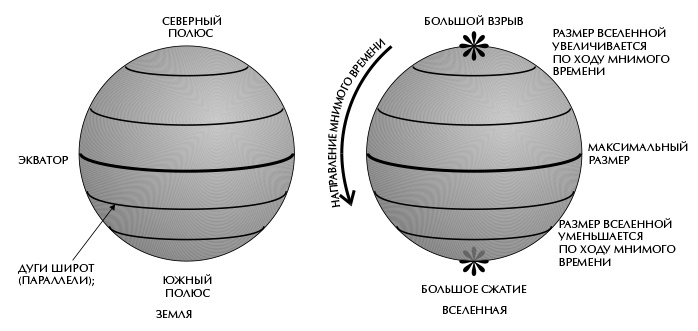
Рис. 8.1
А вот в действительном времени история Вселенной будет выглядеть совсем иначе. Примерно 10–20 миллиардов лет назад она имела бы минимальный размер, равный максимальному радиусу траектории в мнимом времени. В более поздние действительные моменты времени Вселенная расширялась по хаотичной инфляционной модели, предложенной Линде (но теперь нет необходимости предполагать, что Вселенная сотворена в некоем требуемом состоянии). Вселенная увеличилась бы до очень большого размера (рис. 8.1), а потом ей предстояло бы снова коллапсировать в нечто, в действительном времени имеющее вид сингулярности. Так что в некотором смысле мы все равно обречены, даже если будем держаться подальше от черных дыр. Сингулярностей нет, только если представить историю Вселенной в мнимом времени.
Если Вселенная действительно находится в таком квантовом состоянии, то в мнимом времени в ее истории не должно быть сингулярностей. Поэтому может показаться, что мои недавние работы полностью перечеркивают результаты моих более ранних работ о сингулярностях. Но, как я отметил выше, прикладное значение теорем о сингулярностях в другом: они показали, что гравитационное поле должно быть настолько сильным, чтобы нельзя было более пренебрегать квантовыми эффектами. Это, в свою очередь, привело меня к мысли, что в мнимом времени Вселенная может быть конечной, но не иметь границ и сингулярностей. При переходе к действительному времени, в котором мы существуем, сингулярности все же появляются. Бедного астронавта, падающего в черную дыру, ждет печальный конец. Он не встретил бы никаких сингулярностей, только если бы жил во мнимом времени.
Исходя из сказанного, кто-то может заключить, будто так называемое мнимое время на самом деле и есть действительное, реальное время, а то, что мы называем действительным временем, – всего лишь плод нашего воображения. В действительном времени у Вселенной есть начало и конец – они находятся в сингулярностях, образующих границы пространства-времени, где законы физики перестают действовать. Но во мнимом времени нет ни сингулярностей, ни границ. Так что не исключено, что время, называемое нами мнимым, в действительности более фундаментально, а то, что мы называем действительным временем, – всего лишь концепция, и мы придумали ее, чтобы описать, как, на наш взгляд, выглядит Вселенная. Но вспомним, о чем говорилось в главе 1: научная теория – это всего лишь математическая модель, созданная для описания наших наблюдений; она существует только в нашем воображении. Так что, может быть, вопрос «Что реально – действительное или мнимое время?» вообще не имеет смысла. Это всего только вопрос выбора – выбора более удобного инструмента для описания.
Можно также применить суммирование по траекториям, имея в виду и гипотезу об отсутствии границ – чтобы установить, какие свойства Вселенной, вероятнее всего, встречаются одновременно. Например, можно рассчитать вероятность того, что Вселенная расширяется с почти одинаковой скоростью во всех направлениях в эпоху, когда ее плотность равна современному значению. В рассмотренных до сих пор упрощенных моделях эта вероятность оказывается высокой. То есть из условия отсутствия границ с очень высокой вероятностью следует, что современная скорость расширения Вселенной практически одинакова во всех направлениях [38]. Это находится в согласии с результатами наблюдений реликтового излучения: интенсивность этого излучения практически одинакова во всех направлениях. Если бы Вселенная в некоторых направлениях расширялась быстрее, чем в других, то интенсивность излучения в этих направлениях была бы ниже из-за дополнительного красного смещения.
