Спустя некоторое время после вышеупомянутого открытия – того свойства, что площадь горизонта событий возрастает при попадании вещества в черную дыру, – аспирант Принстонского университета Яаков Бекенштейн предположил, что площадь горизонта событий может служить мерой энтропии черной дыры. При попадании вещества-носителя энтропии в черную дыру площадь ее горизонта событий возрастает, причем сумма энтропии вещества вне черных дыр и площадей горизонтов никогда не уменьшается.
Эта гипотеза, похоже, позволяла в большинстве случаев избежать нарушения второго начала термодинамики. Однако у нее был очень существенный недостаток. Если черная дыра обладает энтропией, то у нее должна также быть и температура. А тело с определенной температурой должно быть источником излучения определенной интенсивности. Повседневный опыт подсказывает, что если нагреть кочергу на огне, она докрасна раскаляется и излучает свет. При этом тела с более низкой температурой излучают тоже, но мы не замечаем этого, поскольку их излучение весьма слабое. Излучение – обязательное условие, помогающее избежать нарушения второго начала термодинамики. Поэтому черные дыры должны излучать. Но по самому определению черные дыры – это объекты, ничего не возвращающие в мир за своими пределами. Поэтому площадь горизонта событий черной дыры не может считаться ее энтропией. В 1972 году мы вместе с Брэндоном Картером и американским коллегой Джимом Бардином написали статью, в которой обратили внимание, что несмотря на большое сходство между энтропией и площадью горизонта событий, имеет место упомянутая выше неразрешимая проблема. Должен признаться, что я писал эту статью, в частности, под влиянием своего недовольства Бекенштейном, который, как мне казалось, превратно понял суть открытого мной увеличения площади горизонта событий. Но оказалось, что он в целом был прав, хотя его мысль обрела неожиданное для него самого звучание.
В сентябре 1973 года я посетил Москву, где беседовал о черных дырах с ведущими советскими учеными – Яковом Зельдовичем и Алексеем Старобинским. Они убедили меня, что согласно принципу неопределенности квантовой механики вращающиеся черные дыры должны порождать и излучать частицы. Их доводы показались мне убедительными с физической точки зрения, но мне не понравились математические приемы, которыми Зельдович и Старобинский пользовались для описания свойств этого излучения. Поэтому я занялся разработкой более совершенной математической методики и в конце ноября 1973 года представил ее на неформальном семинаре в Оксфорде. В то время я еще не выполнил расчеты и не определил фактическое количество излучаемых частиц. Я ожидал получить именно то излучение, которое Зельдович и Старобинский предсказали в случае вращающихся черных дыр. Завершив вычисления, к удивлению и досаде, я обнаружил, что даже невращающиеся черные дыры должны порождать и излучать частицы с постоянным темпом. Сначала я решил, что полученное излучение свидетельствовало о недопустимости одного из приближений, к которым мне пришлось прибегнуть. Я опасался, что если об этом узнает Бекенштейн, он будет использовать это как довод в пользу своих идей об энтропии черной дыры, которая мне очень не нравилась. Но чем больше я размышлял над этим, тем больше укреплялся во мнении, что мои приближения верны. Окончательно в реальности излучения меня убедил тот факт, что вычисленный спектр излученных частиц в точности соответствовал спектру излучения нагретого тела и что черная дыра излучала частицы как раз с таким темпом, при котором не нарушалось второе начало термодинамики. С тех пор разные люди в разных формах выполнили те же расчеты. И они подтвердили, что черная дыра должна испускать частицы и излучение точно так, как если бы она представляла собой нагретое тело, температура которого зависит только от его массы: чем больше масса, тем ниже температура.
Как же черная дыра умудряется испускать частицы, когда известно, что ничто не может уйти из-под ее горизонта событий? Квантовая механика отвечает на этот вопрос так: частицы появляются не из «нутра» черной дыры, а из «пустого» пространства сразу за горизонтом событий. Это следует понимать следующим образом: пространство, которое мы считаем «пустым», не может быть таковым в действительности, потому что это означало бы, что все поля, включая электромагнитное и гравитационное, должны быть равны нулю. Но величина поля и скорость его изменения со временем сходны с положением и скоростью частицы: согласно принципу неопределенности, чем точнее одна из этих величин, тем с меньшей точностью мы можем рассчитать другую. Так, в «пустом» пространстве поле не может быть в точности равно нулю, поскольку в этом случае оно имело бы точное значение (нулевое) и точную скорость изменения (тоже нулевую). Величина поля должна содержать некоторую минимальную неопределенность, или квантовые флуктуации. Эти флуктуации можно рассматривать как пары частиц света или гравитации, которые совместно рождаются в некоторое время, расходятся, а затем снова сходятся и взаимно аннигилируют. Это виртуальные частицы, аналогичные тем, что переносят гравитационную силу Солнца: в отличие от реальных частиц, их невозможно обнаружить непосредственно – с помощью детектора частиц. Но их косвенные проявления – например, небольшие изменения энергии орбит электронов в атомах – поддаются измерению и замечательно согласуются с теоретическими предсказаниями. Из принципа неопределенности также следует возникновение сходных виртуальных пар частиц вещества, таких как электроны и кварки. Но в этом случае один из членов пары должен быть частицей, а второй – античастицей (античастицы света и гравитации совпадают с соответствующими частицами).
Поскольку энергия не может возникать из ничего, то один из членов пары частица/античастица должен иметь положительную энергию, а другой – отрицательную. Обладателю отрицательной энергии суждено быть короткоживущей виртуальной частицей, потому что в нормальных условиях энергия реальных частиц всегда положительна. Посему частице с отрицательной энергией предстоит найти партнера, а им обоим впоследствии – взаимно аннигилировать. Но энергия реальной частицы вблизи массивного тела меньше, чем у частицы на большом удалении, поскольку ее перемещение вдаль в условиях гравитационного притяжения тела требует затрат энергии. В обычных условиях энергия частицы все же остается положительной, но гравитационное поле внутри черной дыры настолько сильно, что даже энергия реальной частицы внутри нее может оказаться отрицательной. Поэтому в присутствии черной дыры виртуальная частица с отрицательной энергией вполне может упасть в нее и превратиться там в реальную частицу или античастицу. В этом случае она больше не обязана взаимно аннигилировать со своей парой. Покинутый партнер может также упасть в черную дыру или, если он обладает положительной энергией, покинуть ее окрестности в виде реальной частицы или античастицы (рис. 7.4). Удаленный наблюдатель примет эту частицу за излученную черной дырой. Чем меньше черная дыра, тем меньшее расстояние частица с отрицательной энергией должна пройти, прежде чем стать реальной, и следовательно, тем выше темп излучения – а также эффективная температура – черной дыры.
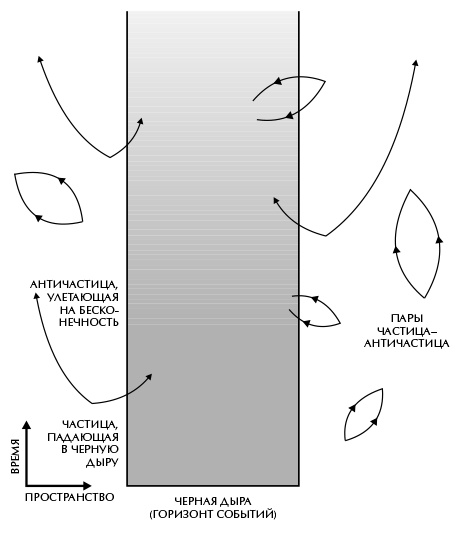
Рис. 7.4
Положительная энергия исходящего излучения уравновешивается потоком частиц отрицательной энергии, направленным внутрь черной дыры. В соответствии с уравнением Эйнштейна E = mc2 (где E – энергия, m – масса, а c – скорость света) энергия пропорциональна массе. Следовательно, поток отрицательной энергии в черную дыру приводит к уменьшению ее массы. По мере уменьшения массы уменьшается и площадь горизонта событий, однако уменьшение энтропии черной дыры в полной мере компенсируется энтропией испускаемого ею излучения, и таким образом, второе начало термодинамики не нарушается.



