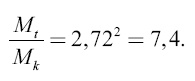
Это значит, что вес заряда должен составлять
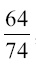 , то есть 87 % веса ракеты.
, то есть 87 % веса ракеты.
Вот несколько частных случаев.
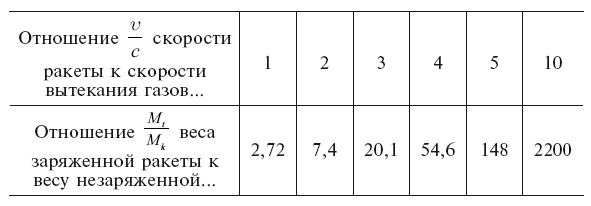
Практически идти далеко в смысле увеличения скорости ракеты, как видим, в реальных условиях не удастся: числа второй строки растут чересчур стремительно.
Если бы мы пожелали, например, добиться скорости ракеты в 20 раз большей скорости вытекания газов, нам пришлось бы зарядить ее количеством горючего, которое в 50 миллионов раз больше веса незаряженной ракеты! Напомним, что в цистерне с керосином содержимое только в 13 раз тяжелее тары; даже в пчелиной ячейке мед весит всего в 60 раз больше, чем восковая оболочка. Технике никогда, вероятно, не удастся соорудить ракету, которая в заряженном состоянии превышала бы вес незаряженной ракеты хотя бы только в 100 или даже в 50 раз. Едва ли поэтому придется на практике иметь дело со скоростями ракеты, превышающими скорость продуктов горения более чем в 4 раза. Отсюда понятно, как важно для развития ракетного дела добиться большей скорости вытекания газов. Каждая лишняя сотня метров скорости отброса создает заметную экономию в грузе горючего, который берет с собой ракета.
Еще раз подтверждается необходимость перехода от пороха к горючим жидкостям для достижения значительных скоростей полета. Если для ракет земного назначения порох оказывается еще достаточно энергоемким зарядом, то для перелетов космических он уже совсем непригоден. В виде примера сделаем два расчета.
1. Какой заряд пороха необходим ракете, предназначаемой для переброски бомбы в 50 кг весом с максимальной скоростью 500 м/с?
Пусть скорость вытекания пороховых газов из дюзы равна 1000 м/с. Если искомый заряд х, то по формуле Циолковского:
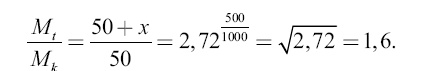
Легко вычислить, что x = 30 кг. При скорости вытекания пороховых газов 2000 м/с достаточен для этого еще меньший заряд – 14 кг.
2. Какой заряд необходим для переброски 1 т полезного груза с Земли на Луну?
Чтобы долететь до Луны с наименьшим расходом горючего, ракета должна быть снабжена запасом энергии, отвечающим скорости 12 240 м/с (см. Приложение 4). Возьмем наибольшую скорость вытекания пороховых газов 2400 м/с и составим уравнение:
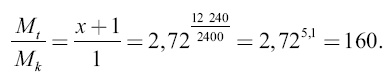
Отсюда x = 159. Заряд должен составлять
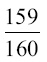 веса ракеты; на всю долю полезного груза остается 0,6 % общего веса. Излишне говорить, что это конструктивно неосуществимо.
веса ракеты; на всю долю полезного груза остается 0,6 % общего веса. Излишне говорить, что это конструктивно неосуществимо.
Пользуясь же жидким горючим, со скоростью вытекания газов 4000 м/с, мы получаем гораздо более благоприятные соотношения:
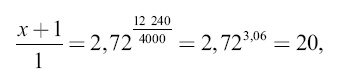
откуда x = 19. Заряд составляет
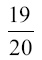 общего веса, и на долю полезного груза приходится уже 5 %.
общего веса, и на долю полезного груза приходится уже 5 %.
Читателю должна быть понятна теперь та задача, которую поставили перед собой работники звездоплавания на нынешнем этапе его развития: во что бы то ни стало изобрести ракету с жидким зарядом. Будущее имеют только такие ракеты; без них заманчивые цели звездоплавания никогда не будут претворены в действительность. В дальнейших главах мы побеседуем о результатах этих изобретательских стремлений.
Перейдем теперь к следующему пункту механики реактивного движения. Как вычислить силу, с какой продукты горения давят на ракету? Для этого достаточно знать количество ежесекундно потребляемого горючего и скорость вытекания газов. Расчет основан на элементарных положениях динамики. По закону противодействия количество движения (mc), присущее вытекающим газам, в каждый момент равно количеству движения (Mυ) самой ракеты. Последнее же равно импульсу силы, увлекающей ракету (Ft = Mυ). Значит (считая t = 1 с), имеем, что искомая сила напора на ракету равна
F = mc,
где m — масса ежесекундно потребляемого горючего, а c — секундная скорость газовой струи. Если, например, ракета сжигает 160 г бензина в секунду, а продукты сгорания вытекают со скоростью 2000 м/с = 200 000 см/с, то сила напора на ракету (или сила тяги) составляет
160 × 200 000 = 32 000 000 дин = около 32 кг.
Нам предстоит еще рассмотреть вопрос о влиянии силы тяжести на полет ракеты. До сих пор мы вели расчеты в предположении, что земная тяжесть на ракету не действует. Вспомним, однако, что под влиянием земной тяжести все тела близ поверхности Земли падают с секундным ускорением около 10 м/с. Отсюда прямо следует, что если ракета должна в среде без тяжести получить движение отвесно вверх с секундным ускорением 40 м/с, то, взлетая от Земли, она получит ускорение всего в 30 м/с2. Далее, если собственное ускорение ракеты меньше ускорения земной тяжести, то такая ракета вовсе не будет подниматься на Земле, как бы долго ни продолжалось горение и сколько бы горючего ни было израсходовано. Наконец в случае равенства обоих ускорений ракета представляет картину совершенно необычайную: она неподвижно висит над Землей все время, пока происходит горение, а по окончании его падает на Землю.
Как видим, быстрота сгорания, обусловливающая нарастание скорости ракеты, определяет в среде тяжести судьбу ракеты; если горение идет слишком медленным темпом, отлет ракеты вовсе не состоится. Математическое рассмотрение вопроса (см. Приложение 3) показывает, что в условиях тяжести скорость отвесного поднятия ракеты всегда несколько меньше той, какую получила бы ракета, израсходовав равный запас горючего в среде без тяжести. Чем больше собственное ускорение ракеты по сравнению с ускорением тяжести, тем меньше различие между скоростью ракеты в среде без тяжести и в условиях тяжести. Но так как человеческий организм может безопасно переносить не более чем трехкратное увеличение земной тяжести, то при отлете с Земли придется практически весьма считаться с этим различием.



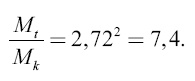
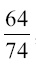 , то есть 87 % веса ракеты.
, то есть 87 % веса ракеты.
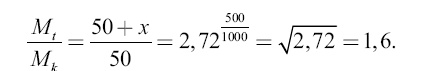
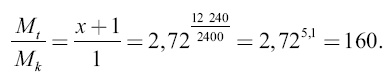
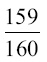 веса ракеты; на всю долю полезного груза остается 0,6 % общего веса. Излишне говорить, что это конструктивно неосуществимо.
веса ракеты; на всю долю полезного груза остается 0,6 % общего веса. Излишне говорить, что это конструктивно неосуществимо.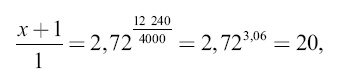
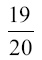 общего веса, и на долю полезного груза приходится уже 5 %.
общего веса, и на долю полезного груза приходится уже 5 %.