Глава 13
Механика полета ракеты
Мы подошли к другой стороне механики ракеты: к вопросу о том, от каких обстоятельств зависит окончательная скорость ракеты и – что не менее важно уяснить себе – от каких обстоятельств она не зависит. Теоретический вывод этих соотношений дан в конце книги. Здесь приводим лишь окончательный результат.
Математический анализ устанавливает, что вереде без тяжести (для простоты пока отвлекаемся от тяжести) окончательная скорость, приобретаемая ракетой после горения, зависит только от двух обстоятельств:
1) от той скорости, с какой вытекают из ее сопла газообразные продукты горения;
2) от отношения первоначальной массы ракеты к ее окончательной массе, то есть отношения массы ракеты до горения к массе ее после горения.
Если первоначальную массу ракеты вместе с запасом горючего обозначим через Мt, а конечную массу, когда заряд выгорит, – через Мk, то скорость, приобретаемая ракетой к концу горения, зависит от величины дроби:
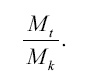
Ни от каких других причин окончательная скорость ракеты в среде без тяжести не зависит. Это – замечательный результат. Оказывается, что продолжительность и порядок горения нисколько не влияют на величину приобретаемой ракетой скорости: «Происходит ли горение равномерно или нет, длится ли оно секунды или тысячелетия – это все равно; даже перерывы ничего не значат» (Циолковский). Второй поучительный вывод тот, что скорость ракеты не обусловливается вовсе, как можно было бы ожидать, абсолютным количеством сожженных веществ; она зависит лишь от отношения массы этих веществ к массе незаряженной (вернее, разряженной) ракеты. Маленькая ракета, заряженная несколькими граммами горючего, может приобрести такую же окончательную скорость, как и исполинская ракета с зарядом в сотни или тысячи тонн, если только окончательная масса ракеты в обоих случаях составляет одинаковую долю первоначальной.
Читатель должен также отрешиться от распространенного представления о ракете как об аппарате, отталкивающемся от воздуха. Это странное ходячее мнение потому так живуче, что для поверхностного суждения кажется естественным и бесспорным. Хотя правильный взгляд на механизм полета ракеты установился уже в эпоху Ньютона, заблуждение это владеет большинством умов еще и в наши дни, мешая правильно разбираться в вопросах ракетного летания.
Уместно остановиться здесь и на другом заблуждении более тонкого характера. Против возможности межпланетных перелетов выдвигается нередко следующий довод. На земном шаре не существует такого горючего, энергия которого, превращенная в механическую работу, была бы достаточна для переноса его самого хотя бы на Луну. Килограмм наиболее энергоемкого горючего – смеси водорода с кислородом – развивает не более 2900 × 427, то есть 1 240 000 кгм. Между тем, чтобы удалить 1 кг вещества с земной поверхности на расстояние до Луны, требуется совершить работу свыше 6 000 000 кгм. Отсюда делают поспешный вывод, что горючее, которое не может даже самого себя унести на Луну, тем более бессильно доставить туда еще какой-нибудь груз. Значит, межпланетные путешествия – несбыточная мечта; все стремления ее осуществить обречены на полную неудачу.
Рассуждения подобного рода, хотя и высказываются зачастую сведущими в других отношениях авторами, свидетельствуют о полном незнакомстве с условиями работы ракеты. Забывают, что ракета вовсе не несет с собой запаса горючего на протяжении всего пути. Она сжигает и отбрасывает свое горючее еще вблизи Земли, в первые несколько минут полета; весь же остальной путь ракета летит за счет энергии, запасенной в течение этих немногих минут горения. Кроме того, надо помнить, что межпланетная ракета расходует массу горючего, значительно превосходящую массу полезного груза ракеты.
Обратимся теперь к языку математических формул, чтобы отчетливее охватить условия движения ракеты. Обозначим, как прежде, начальную массу ракеты, то есть массу ее вместе с зарядом, через Mt; массу ракеты после израсходования заряда, то есть ее конечную массу, буквою Мk. Скорость, с какою продукты сгорания удаляются от летящей ракеты, обозначим буквою с. Наконец, скорость, приобретаемую самой ракетой по израсходованию запаса горючего (в количестве Мt – Мk), обозначим через υ
Между этими четырьмя величинами Mt, Мk, с и υ существует зависимость, впервые установленная К.Э. Циолковским; мы вправе называть ее «формула Циолковского». А именно: для всякой ракеты, летящей в пустоте и в среде без тяжести, справедливо следующее равенство (уравнение ракеты):
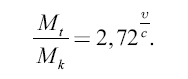
Значение букв, входящих в уравнение ракеты, нам известно. Что же касается числа 2,72, то знакомые с математикой, конечно, узнают в нем основание натуральных логарифмов (е = 2,71828…).
Рассмотрим несколько следствий из этого уравнения
[29].
Прежде всего мы видим, что ракета может двигаться во много раз быстрее продуктов сгорания – в противоположность пушечному снаряду, который не может мчаться быстрее, чем толкающие его пороховые газы. Действительно, если мы желаем, чтобы ракета двигалась в 10 раз быстрее вытекающих из нее газов, то есть чтобы отношение
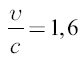 равнялось 10, мы должны положить в формуле ракеты
равнялось 10, мы должны положить в формуле ракеты
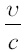 тогда
тогда
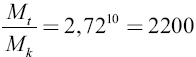 , то есть заряженная ракета должна быть в 2200 раз тяжелее незаряженной; или, иными словами, заряд должен по весу составлять
, то есть заряженная ракета должна быть в 2200 раз тяжелее незаряженной; или, иными словами, заряд должен по весу составлять
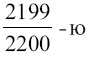 долю веса ракеты. Теоретически это возможно, практически же, конечно, неосуществимо. При меньших значениях
долю веса ракеты. Теоретически это возможно, практически же, конечно, неосуществимо. При меньших значениях
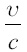 получаются для
получаются для
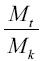 более благоприятные соотношения. Так, если скорость ракеты должна только вдвое превышать скорость вытекающих газов, то отношение
более благоприятные соотношения. Так, если скорость ракеты должна только вдвое превышать скорость вытекающих газов, то отношение



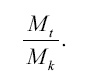
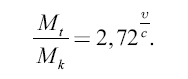
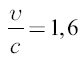 равнялось 10, мы должны положить в формуле ракеты
равнялось 10, мы должны положить в формуле ракеты
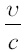 тогда
тогда
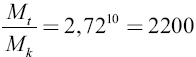 , то есть заряженная ракета должна быть в 2200 раз тяжелее незаряженной; или, иными словами, заряд должен по весу составлять
, то есть заряженная ракета должна быть в 2200 раз тяжелее незаряженной; или, иными словами, заряд должен по весу составлять
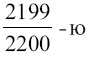 долю веса ракеты. Теоретически это возможно, практически же, конечно, неосуществимо. При меньших значениях
долю веса ракеты. Теоретически это возможно, практически же, конечно, неосуществимо. При меньших значениях
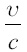 получаются для
получаются для
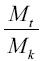 более благоприятные соотношения. Так, если скорость ракеты должна только вдвое превышать скорость вытекающих газов, то отношение
более благоприятные соотношения. Так, если скорость ракеты должна только вдвое превышать скорость вытекающих газов, то отношение