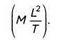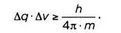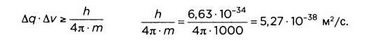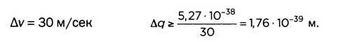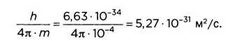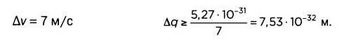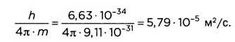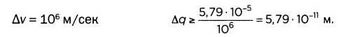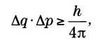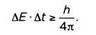Можно попробовать уменьшить энергию света, чтобы сократить воздействие на электрон и избежать значительного изменения его траектории. Согласно формуле Планка (Е = h х v), уменьшение энергии света происходит путем снижения частоты или удлинения электромагнитных волн, что одно и то же. Но эта стратегия не срабатывает. Четкость изображения (оно формируется с помощью электромагнитных волн) зависит от длины волны, которая с ним взаимодействует. Чем сильнее волны удлиняются, тем более размытой становится картинка, которую они дают. Это какой-то заговор! Мы способны или определить траекторию электрона, но при этом сам факт наблюдения эту траекторию нарушает, или сделать так, чтобы энергия не влияла на траекторию частицы, но при этом мы не сможем частицу рассмотреть.
Вернемся к примеру с теннисным кортом. Предположим, что у нас есть очень простой прибор, позволяющий менять длину волны света, с которой мы хотели бы смотреть соревнования. В принципе, на короткий период мы можем обеспечить достаточную четкость изображения, но фотоны толкают мяч с такой силой, что световые частицы, проходящие перед нашими глазами, не могут зафиксировать его положение. Будем увеличивать длину световой волны, снижая таким образом их влияние на мяч. Изображение корта станет более размытым. В тот момент, когда начинает вырисовываться траектория мяча, мы превысим допустимое разрешение и снова окажемся погруженными в квантовый туман. Как видите, существует степень неопределенности, присущая наблюдению, которую нельзя уменьшить. А все потому, что свет (измеряющий субъект) и электрон (измеряемый объект) являются квантовыми сущностями, которые воздействуют друг на друга.
Неопределенность в цифрах
Возьмем отношение Δq · Δρ => h/4π, которое можно переформулировать, используя Δν, при этом р=m • у:
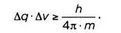
Неравенство показывает, что граница неопределенности для q и v зависит от отношения между постоянной Планка и массой т. Более того, для макроскопических объектов h будет незначительной, следовательно, Δq и Δρ тоже могут иметь малые значения. Таким образом, создается впечатление, что мы можем определить результат с желаемой точностью. Но с того момента как масса и размер приближаются к постоянной Планка, неопределенности начинают выходить на первый план. Чтобы доказать это, применим отношения неопределенности к трем различным объектам.
1. Автомобиль. Примем его массу примерно равной одной тонне:
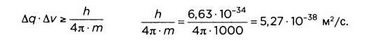
Предположим, что автомобиль перемещается со скоростью 100 км/час (около 30 м/сек):
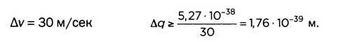
Разница между размером машины, который измеряется в метрах, и неопределенностью положения равна единице с 39 нулями перед ней. Невообразимо мало.
2. Пчела массой ОД грамма:
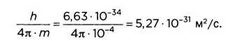
Это насекомое может перемещаться с максимальной скоростью 7 м/с:
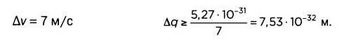
Для пчелы длиной несколько сантиметров масштаб разницы между неопределенностью ее положения и размером — 10~30. Это очень мало.
3. Электрон массой около 9,11 х 10-31 кг:
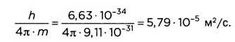
Присвоим электрону среднюю скорость 10 6 м/сек, или примерно 1% от скорости света:
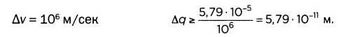
Радиус орбиты электрона водорода в фундаментальном состоянии (модель Бора), как правило, является величиной, лежащей в основе модели атома. Как мы уже увидели, радиус соответствует волновой функции Шрёдингера для той же энергии. Его значение r = 5,29 х 10-11 метров. Таким образом, в случае с электроном, неопределенность его положения — одного порядка с размером места, в котором он находится: невозможно его отследить.
Мы рассмотрели конкретный случай, но подобная неопределенность может наблюдаться в любом экспериментальном контексте. Физики обозначают степень неопределенности измерения с помощью символа Δ. Таким образом, Δx = 0 означает, что пространственная координатах частицы может иметь лишь одно значение, то есть положение частицы четко зафиксировано. Однако Δx = 5 означает, что частица может находиться где угодно в радиусе 5 метров. Гейзенберг не был удовлетворен изучением неопределенности и определил ее границы при помощи постоянной Планка:
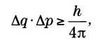
где q означает положение частицы, а р — ее импульс. Речь идет о принципе неопределенности, в котором объединены две различные физики, и наше знание об одной обнаруживается через информированность о другой.
Заразительность неопределенности
Помимо импульса и положения, Гейзенберг присвоил свое соотношение неопределенности другим парам сопряженных величин, произведение которых измеряется в тех же единицах, что и действие, то есть, подобно постоянной Планка, определяется как произведение энергии на время:
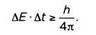
М, L и Т— фундаментальные физические величины (масса, длина и время). Считается, что произведение времени на энергию выражается в тех же единицах, что и произведение длины на импульс, а также постоянная Планка: