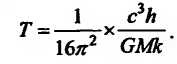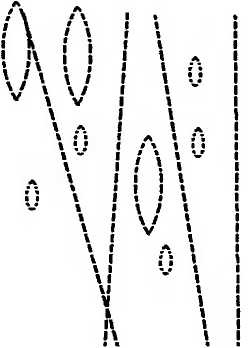
Реальные фотоны — это прямые пунктирные линии. Их присутствие указывает на теплоту и тепловую дрожь. Но если пространство находится при абсолютном нуле, реальных фотонов не будет. Остаются лишь микроскопические петли виртуальных фотонов, которые быстрыми вспышками обретают и утрачивают существование. Пары виртуальных фотонов составляют часть вакуума — того, что мы называем пустым пространством, — даже когда температура равна абсолютному нулю.
В обычных условиях два типа дрожи нельзя спутать. Однако горизонт черной дыры — вещь необычная. Вблизи горизонта эти два типа флуктуаций начинают смешиваться таким способом, которого никто никогда не ожидал. Чтобы получить представление о том, как это происходит, вообразите Алису, свободно падающую в черную дыру в среде, имеющей температуру абсолютного нуля, — в абсолютном вакууме. Она окружена парами виртуальных фотонов, но она их не замечает. Реальных фотонов вокруг нее нет.
Теперь рассмотрим Боба, который висит над горизонтом. Для него все сильно запутывается. Некоторые пары виртуальных фотонов — те, что не замечает Алиса, — могут частично находиться внутри горизонта, а частично вовне. Но частица, находящаяся за горизонтом, лишена всякой связи с Бобом. Он видит лишь один фотон и не может распознать, что он принадлежит виртуальной паре. Верите вы или нет, но такой фотон, застрявший вовне, в то время как его партнер оказался за горизонтом, будет воздействовать на Боба и его кожу в точности так же, как если бы это был обычный тепловой фотон. Вблизи горизонта разделение теплового и квантового зависит от наблюдателя: то, что Алиса воспринимает (или не воспринимает) как квантовый шум, Боб регистрирует как тепловую энергию. В случае черной дыры тепловые и квантовые флуктуации становятся двумя сторонами одной медали. Мы вернемся к этому вопросу в главе 20, когда будем рассматривать Алисин самолет.
Опираясь на математику квантовой теории поля, Хокинг рассчитал, что флуктуации вакуума в присутствии черной дыры приводят к испусканию фотонов, в точности как если бы горизонт черной дыры был горячим черным телом. Эти фотоны называются хокинговским излучением. Самое интересное, что черная дыра излучает так, как будто ее температура примерно равна той, что получилась бы из доказательства Бекенштейна, если бы сам Бекенштейн сделал этот вывод. В действительности Хокинг пошел дальше Бекенштейна; его методы оказались столь аккуратны, что позволили вычислить точную температуру, а по ней и энтропию черной дыры. Бекенштейн утверждал лишь, что энтропия пропорциональна площади горизонта, измеренной в планковских единицах. Хокингу уже не требовалось использовать неопределенный термин «пропорциональна». Согласно его расчетам, энтропия черной дыры в точности равна одной четверти площади горизонта, измеренной в планковских единицах.
Кстати, выведенное Хокингом уравнение для температуры черной дыры как раз и было на доске, когда я пришел на лекцию Скиамы:
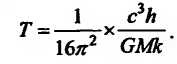
Обратите внимание, что в формуле Хокинга масса черной дыры стоит в знаменателе. Это значит, что чем больше масса, тем холоднее черная дыра, и наоборот: чем меньше масса, тем черная дыра теплее.
Давайте применим эту формулу к какой-нибудь черной дыре. Вот значения всех постоянных
[82]:
с = 3 х108
G = 6,7x10-11
Н = 7х10-34
k = 1,4x10-23.
Рассмотрим случай звезды с массой в пять раз больше солнечной, которая в конечном счете коллапсирует в черную дыру. Ее масса в килограммах будет:
М = 1031.
Если подставить все эти числа в формулу Хокинга, получится, что температура черной дыры составляет 10-8 градусов Кельвина. Это очень низкая температура — всего десять миллиардных градуса над абсолютным нулем! В природе нет ничего столь холодного. Межзвездное и даже межгалактическое пространство намного теплее.
Еще более холодные черные дыры находятся в центрах галактик. Будучи в миллиард раз массивнее звездных черных дыр, они в миллиард раз больше и в миллиард раз холоднее. Но можно представить себе и гораздо меньшие черные дыры. Допустим, какой-то катаклизм сжал Землю. Ее масса примерно в миллион раз меньше массы звезды. Получившаяся черная дыра будет иметь колоссальную температуру — около 0,01 градуса над абсолютным нулем: намного теплее звездной черной дыры, но все равно ужасно холодно — холоднее жидкого гелия и намного холоднее замерзшего кислорода. Черная дыра с массой Луны разогреется уже до 1 градуса Кельвина.
Но рассмотрим теперь, что происходит, когда черная дыра испускает хокинговское излучение и испаряется. По мере уменьшения массы черная дыра сжимается, а ее температура растет. Со временем черная дыра становится горячей. К тому моменту, когда ее масса становится с большой валун, температура вырастет до миллиарда миллиардов градусов. А при достижении планковской массы температура поднимется до 1032 градусов. Единственное место и время, когда во Вселенной могла быть подобная температура, — это самое начало Большого взрыва.
Расчеты Хокинга, показывающие, как испаряются черные дыры, — это настоящее чудо изобретательности. Я думаю, что к тому времени, когда их следствия будут вполне поняты, физики станут рассматривать их как начало великой научной революции. Еще слишком рано точно предсказывать, чем обернется эта революция, но она затронет очень глубокие вопросы: природу пространства-времени, роль элементарных частиц и загадки происхождения Вселенной. Ученые задаются вопросом: принадлежит ли Хокинг к числу величайших физиков всех времен и каково его место в этой иерархии. Тем, кто сомневается в величии Хокинга, я просто предлагаю прочитать его статью 1975 года «Рождение частиц черными дырами».
Но как бы Стивен Хокинг ни был велик, по крайней мере однажды он сбился с пути, и именно с этого началась Битва при черной дыре.
Часть II
Неожиданная атака
10
Как Стивен потерял свои биты и не знал, где их найти
В моем изложении событий есть что-то неправдоподобное — следовательно, я допустил ошибку.