Приведенное выше наблюдение нельзя назвать скромным или незначительным: оно имеет очень важные последствия, поскольку существует лишь два возможных способа подведения и уменьшения циферблатов, прежде чем сложить их, в результате чего получится конечный циферблат со свойствами, не зависящими от того, какой из исходных циферблатов подвергся обработке. Это показано на рис. 7.4. Верхняя половина рисунка иллюстрирует, что если подкрутить циферблат 1 на 90° и прибавить его к циферблату 2, то получившийся циферблат будет не равен по размеру тому, который получится, если подкрутить на 90° циферблат 2 и прибавить его к циферблату 1. Это можно видеть, потому что, если сначала подкрутить циферблат 1, то новая стрелка, которая показана здесь пунктиром, будет показывать в противоположном по отношению к стрелке циферблата 2 направлении, таким образом частично отменяя этот циферблат. При смещении же циферблата 2 его стрелка продолжает указывать в том же направлении, что и стрелка циферблата 1, так что они прибавляются, образуя более длинную стрелку.
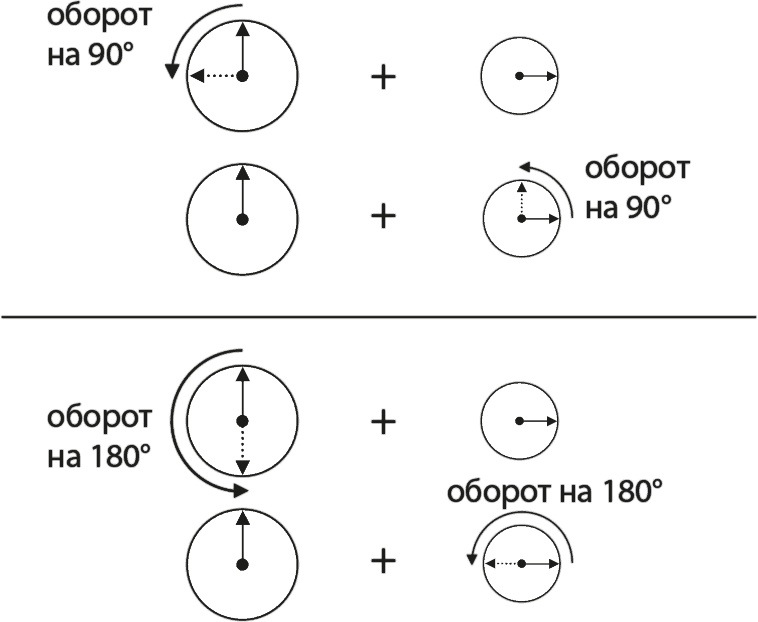
Рис. 7.4. Верхняя часть рисунка показывает, что сложение циферблатов 1 и 2 после смещения циферблата 1 на 90° не эквивалентно их сложению после смещения на те же 90° циферблата 2. Нижняя часть показывает интересную возможность смещения одного из циферблатов на 180° перед сложением
Должно быть ясно, что 90° – это не какой-то особый случай, и другие углы тоже дадут циферблаты, которые зависят от того, который из двух исходных мы предпочли подкрутить.
Очевидное исключение – это перевод стрелки часов на 0°, потому что смещение циферблата 1 на 0° с последующим его сложением с циферблатом 2 – это, разумеется, то же самое, что и смещение циферблата 2 на 0° с последующим его сложением с циферблатом 1. Это значит, что сложение циферблатов без всякого перевода их стрелок – это вполне жизнеспособная возможность. Точно так же подойдет и подведение обоих циферблатов на одну и ту же величину, но это фактически та же ситуация, что и случай «без смещения»: нужно просто переопределить то, что мы будем называть «12 часами». Это равноценно утверждению, что мы всегда можем смещать любой циферблат на определенную величину, если эта величина равна для всех циферблатов. Это никогда не будет оказывать воздействие на те вероятности, которые мы пытаемся подсчитать.
Нижняя часть рис. 7.4 показывает, что, как бы странно это ни звучало, есть еще один способ сочетания циферблатов: мы можем повернуть один из них на 180° с последующим их сложением. Не получается один и тот же циферблат в двух случаях, но размер при этом остается тем же самым, следовательно, это приводит к той же самой вероятности нахождения одного электрона в точке А и другого в точке В.
Подобные рассуждения можно привести и по поводу возможности сжатия или расширения одного из циферблатов перед их сложением, потому что если мы сожмем циферблат 1 на определенную величину, прежде чем прибавить его к циферблату 2, то получаться будет не тот результат, что при сжатии циферблата 2 на ту же величину перед сложением его с циферблатом 1, и исключений у этого правила нет.
Итак, можно сделать интересный вывод. Хотя мы начали с того, что даровали себе полную свободу действий, оказалось, что, поскольку нет возможности отличить частицы друг от друга, есть лишь два способа сочетания циферблатов: мы можем сложить их либо сразу, либо после поворота стрелки одного из них на 180°. И самое замечательное, что природа идет обоими путями.
В случае с электронами перед сложением циферблатов нужно произвести лишний оборот. В случае с фотонами или бозонами Хиггса нужно сложить циферблаты, не прибегая к повороту. Итак, частицы природы делятся на два типа: те, которым нужен лишний оборот, называются фермионами, а те, которые обходятся без него, именуются бозонами.
Что определяет, фермион конкретная частица или бозон? Ее спин. Спин, как можно догадаться по этимологии слова (от англ. spin – «вращать»), – это мера углового момента частицы, и фермионы всегда имеют спин, равный полуцелому числу
[34], а у бозонов спин целый. Мы говорим, что у электрона спин равен ½, у фотона – 1, а у бозона Хиггса – 0. Не хотим вдаваться в подробности по поводу спина, потому что они в основном чисто технические. Однако в разговоре о периодической системе оказалось важно, что в результате электроны делятся на два типа в соответствии с двумя возможными значениями их углового момента (спин, направленный вверх, или спин, направленный вниз). Это пример общего правила, которое гласит: частицы со спином s обычно имеют 2s + 1 типов, например частицы со спином ½ (то есть электроны) имеют два типа, со спином 1 – три типа, а со спином 0 – один тип.
Взаимосвязь между угловым моментом частицы и нашим способом сочетания часов известна как теорема Паули, или теорема о связи спина со статистикой. Она выводится в том случае, когда формулировка квантовой теории согласуется со специальной теорией относительности Эйнштейна. Точнее говоря, это прямой результат выполнения причинно-следственных законов. К сожалению, выведение теоремы о связи спина со статистикой лежит за пределами уровня этой книги – как, честно говоря, и многих других. В «Фейнмановских лекциях по физике» автору пришлось сказать следующее:
«Мы просим прощения за то, что неспособны элементарно объяснить вам это. Но объяснение существует, его нашел Паули, основываясь на сложных доводах квантовой теории поля и теории относительности. Он показал, что эти факты по необходимости связаны друг с другом; но мы не в состоянии найти способ воспроизвести его аргументы на элементарном уровне. Это, видимо, одно из немногих мест в физике, когда правило формулируется очень просто, хотя столь же простого объяснения ему не найдено».
Вспомнив о том, что Ричард Фейнман вынужден был написать подобное в учебнике университетского уровня, мы можем только поднять руки и сдаться. Но правило само по себе довольно простое, и вам лишь придется поверить нам на слово в его доказательстве: для фермионов поворот необходим, а для бозонов – нет. Судя по всему, поворот служит причиной принципа Паули, а следовательно, и структуры атомов, и теперь, наконец, мы можем дать очень простое объяснение после всей предыдущей кропотливой работы.
Представьте, что точки А и В на рис. 7.3 движутся все ближе и ближе друг к другу. Когда они оказываются совсем близко, циферблат 1 и циферблат 2 должны стать примерно одного размера и показывать примерно одинаковое время. Когда А и В перекрываются, то и циферблаты должны быть идентичными. Это очевидно, поскольку циферблат 1 соответствует частице 1, заканчивающей движение в точке А, а циферблат 2 в этом конкретном случае показывает точно такое же время, поскольку точки А и В перекрываются. Тем не менее циферблатов по-прежнему два, и мы по-прежнему должны их сложить. Но тут и возникает тонкость: для фермионов один из циферблатов должен быть перед сложением повернут на 180°. Это значит, что циферблаты всегда будут показывать точно противоположное время для случая совпадения точек А и В (если на одном будет 12 часов, то на другом 6 часов), так что при сложении всегда будет получаться циферблат нулевого размера. Это замечательный результат, поскольку он означает, что вероятность нахождения двух электронов в одной и той же точке всегда будет равна нулю: законы квантовой физики побуждают их избегать друг друга. Чем ближе они друг к другу, тем меньше получающийся циферблат и, соответственно, вероятность такой близости. Это один из способов формулировки знаменитого принципа Паули: электроны избегают друг друга.



