Доверительные интервалы для 100 бросков монеты, когда математическое ожидание равно 50, а среднеквадратичное отклонение в сигмах равно 5. Длина интервала в одну сигму – от 45 до 55, а интервала в пять сигм – от 25 до 75.
Когда мы делаем измерения, разброс вокруг предсказанного исхода часто имеет форму колокола, что и изображено на рисунке вверху. Здесь мы изобразили вероятность получения различных результатов (в данном примере это количество выпадений орла, когда мы бросаем монетку 100 раз). Кривая достигает максимума при наиболее вероятном значении, которое в данном случае равно 50, но есть некоторый естественный разброс вокруг этого значения. Этот разброс – ширина колоколообразной кривой – и есть неопределенность в прогнозе, то есть ст. Для числа подбросов монеты, равного 100, она равна 5, и тогда мы говорим: «Мы ожидаем, что орел выпадет 50 раз плюс-минус 5».
Сигма хороша тем, что она может трансформироваться в вероятность того, какой реальный результат будет получен (даже несмотря на то, что точная формула очень сложна и, как правило, вы просто ищете число в справочнике). Если мы бросаем монетку 100 раз и от 45 до 55 раз выпадает орел, мы говорим, что результат находится «в интервале одной сигмы», что происходит в 68 % испытаний.
Другими словами, результаты, отличающиеся более чем на одну сигму, мы получаем примерно в 32 % испытаний, что немало, так что в результате, отличающемся на одну сигму, нет ничего, что могло бы насторожить. Вы бы не стали подозревать, что монетка «неправильная», только потому, что в 100 подкидываниях 55 раз выпал орел и 45 решка.
Большие сигмы соответствуют все менее вероятным результатам (при условии, что верна нулевая гипотеза). Если у вас из 100 раз орел выпал 60, это отклонение в две ст, и такое происходит только примерно в 5 % испытаний. Этот результат кажется маловероятным, но не совсем неправдоподобным. Его недостаточно, чтобы отвергнуть нулевую гипотезу, но достаточно, чтобы возбудить некоторые подозрения. Выпадению 65 раз орла соответствовало бы отклонению в три ст, что соответствует вероятности 0,3 %. Эти события случаются довольно редко, и теперь у нас появились законные основания думать, что происходит нечто странное. Если бы у нас выпал орел 75 раз из 100, это бы было отклонением в пять ст, а такие события случаются реже чем один раз на миллион. И тогда мы вправе сделать вывод, что сигнал был не просто статистической флуктуацией, и нулевая гипотеза неверна – монетка попалась явно неправильная.
Сигнал и фон
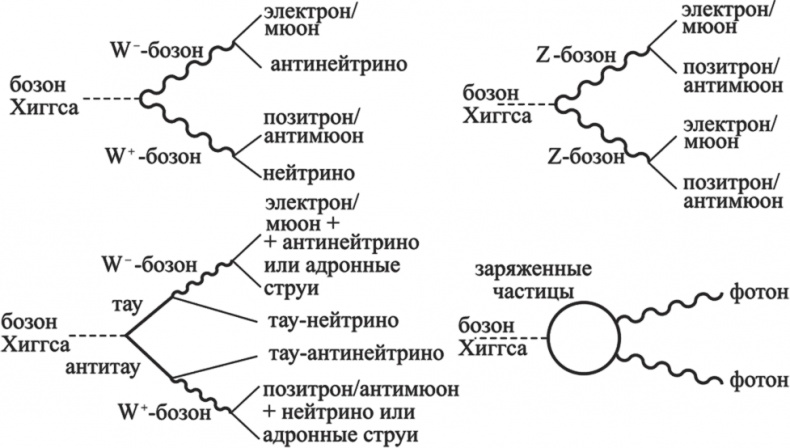
Поскольку физика элементарных частиц управляется квантовой механикой, она очень похожа на подкидывание монетки: самое большее, что мы можем сделать, это предсказывать вероятности. На БАКе мы сталкиваем протоны друг с другом и предсказываем вероятность различных взаимодействий. Для частного случая поиска бозона Хиггса мы рассматриваем различные «каналы», каждый из которых определяется типом частиц, захваченных детекторами. Есть двухфотонный канал, двухлептонный канал, четырехлептонный канал, канал с двумя струями и двумя лептонами, и так далее. В каждом случае мы суммируем энергии вылетающих частиц и с помощью аппарата квантовой теории поля (дополненного реальными измерениями) рассчитываем, сколько событий могли бы ожидать для каждого значения полной энергии. Результаты, как правило, изображаются в виде гладкой кривой.
Наша нулевая гипотеза состоит в том, что бозона Хиггса нет. Если же бозон Хиггса существует, да к тому же обладает какой-то ненулевой массой, основной ожидаемый эффект от него состоит в том, что для соответствующей энергии число событий увеличится. Если масса бозона равна 125 ГэВ, создается некоторое дополнительное количество частиц с суммарной энергией 125 ГэВ, и так далее. Создание бозона Хиггса и его распад обеспечивает механизм (в дополнение ко всем процессам, не связанным с бозоном Хиггса) получения частиц, суммарная энергия которых, как правило, равна массе хиггсовского бозона, что приводит к некоторому количеству дополнительных (по отношению к фону) событий. И мы отправляемся на «сбор шишек» – то есть ищем заметные отклонения от гладкой кривой, которую бы увидели при отсутствии бозона Хиггса.
Мы и не предполагали, что расчет ожидаемого фона будет легкой задачей. Мы, конечно, знаем Стандартную модель, но то, что мы ее знаем, не означает, что рассчитать результат легко. (Стандартной моделью можно описать и атмосферу Земли, но предсказать погоду не так-то просто). С помощью самых совершенных компьютерных алгоритмов ученые моделируют наиболее вероятные исходы протонных столкновений, и эти результаты используются для моделирования работы самих детекторов. И, оценив их усилия, мы охотно признаем, что некоторые вероятности реакций частиц легче измерить, чем просчитать. Чтобы минимизировать влияние человеческого фактора и для лучшего подбора параметров модели часто используется «слепой» анализ, когда каким-то способом скрываются фактические данные в интересующей нас области: либо туда добавляются фиктивные данные, либо просто события в этом «окне» не рассматриваются. Потом добиваются максимально ясного понимания «неинтересных» данных в других областях, и только после того, как это понимание будет достигнуто, открывается «окно», и мы смотрим на экспериментальные данные в той области, где наша частица может скрываться. Подобные манипуляции гарантируют, что мы видим не то, что хотим увидеть, а то, что происходит в действительности.
Так было не всегда. В своей книге «Нобелевские мечты» (Nobel’s Dreams) журналист Гэри Таубес рассказывает об истории исследований Карло Руббиа начала 1980-х годов по обнаружению W– и Z-бозонов, которые принесли ему Нобелевскую премию, а также о его менее успешных попытках получить вторую Нобелевскую премию, за его дерзкие выходы за пределы Стандартной модели. Команда Руббиа использовала при анализе данных по столкновению частиц Megatek – компьютерную систему, которая могла отображать данные на экране компьютера, причем программа позволяла поворачивать изображение вокруг трех координат с помощью джойстика. Заместители Руббиа американец Джеймс Рольф и англичанин Стив Гир стали экспертами в работе на Megatek. Они могли посмотреть на событие, повернуть его немного, отобрать важные треки частиц и уверенно сказать, что они видят – W-, Z-бозон или тау-частицу. «У вас есть эти вычисления, – говорил Руббиа, – но конечная цель всей титанической работы по анализу данных, основная фундаментальная задача должна состоять в том, чтобы дать людям окончательный ответ. И только Джеймс Рольф, глядя на это чертово событие, решит – Z-бозон это или нет». Теперь ситуация изменилась. У нас сейчас гораздо больше данных, но единственный способ понять, что они означают, – пропустить их через компьютер.
Всякий раз, когда возникают некоторая надежда на то, что получен новый экспериментальный результат, первой реакцией становится вопрос: «Сколько сигм?». В физике элементарных частиц неформальный стандарт вырабатывался на протяжении многих лет, и в соответствии с ним отклонение 3σ считается «свидетельством» того, что что-то происходит, в то время как при отклонении в 5σ уже можно объявлять об «открытии» чего-то. Это может показаться излишним требованием, так как фоновое событие 3σ происходит обычно только с вероятностью 0,3 %. Но правильнее было бы рассуждать об этом так: если посмотреть на триста различных измерений, одно из них просто случайно может оказаться событием 3σ! Так что требование придерживаться критерия 5σ является справедливым.

