
Рис. 6.1. Маленькие пузырьки истинного вакуума случайно возникают и расширяются. Пузырьки, которые образовались раньше, вырастают до большего размера.
Именно так происходит, если пузырьки возникают в бешеном темпе и весь процесс распада завершается меньше чем за один период удвоения. Это означает, однако, что инфляция заканчивается слишком быстро, намного раньше, чем вселенная становится однородной и плоской. Нас же интересует противоположный случай, когда темп формирования пузырьков низкий, так что вселенная может расшириться во много раз, прежде чем пузыри начнут сталкиваться. Но, как любил говорить швейцарский физик Пауль Эренфест, здесь-то лягушка и прыгает в воду.
Трудность состоит в том, что пространство между пузырьками заполнено ложным вакуумом, а значит, быстро расширяется. Пузырьки растут очень быстро, со скоростью, близкой к скорости света, но это не сравнится с экспоненциальным расширением ложного вакуума. Если пузырьки не столкнутся в течение одного периода удвоения от момента возникновения, то в дальнейшем расстояние между ними будет только расти, так что они уже никогда не столкнутся.
Выходит, инфляция может никогда не закончиться. Пузыри неограниченно растут в размерах, а в промежутках между ними все продолжают появляться новые. В результате замечательная однородность, порожденная инфляцией, полностью разрушается. Отсутствие подходящего финала для инфляционного расширения стали называть проблемой изящного выхода.
Гут осознал эту проблему спустя несколько месяцев после того, как представил свою новую теорию публике. К тому времени его статья об инфляции еще не была написана, причем по очень простой причине: Алан Гут — самый большой в мире любитель откладывать дела на потом. (Я убедился в этом лично, работая с ним в ряде исследовательских проектов.) Он, конечно, был разочарован, обнаружив в теории серьезный прокол, однако продолжал считать, что идея слишком удачна, чтобы быть ошибочной. Дописав наконец к августу 1980 года свою статью, Гут закончил ее словами: "Я публикую эту статью в надежде, что она… побудит других найти способ обойти нежелательные особенности инфляционного сценария".
[34]
Скалярное поле
Чтобы разобраться в истоках проблемы, давайте подробнее обсудим ложный вакуум. Процесс его распада был изучен гарвардским физиком Сиднеем Коулманом (Sidney Coleman), который описал его в терминах так называемых скалярных полей.
Поле — это количественная характеристика, имеющая определенное значение в каждой точке пространства. Его значения могут меняться от точки к точке, а также во времени. Простым примером поля является температура. Северный полюс, мыс Кейп-Код, центр Солнца — все это точки Вселенной, имеющие определенную температуру. Другой знакомый пример — магнитное поле. В дополнение к величине оно обладает также и направлением. Мы не ощущаем магнитного поля, но его присутствие обнаруживается, если взглянуть на компас. Стрелка указывает направление поля, а его напряженность можно определить по тому, насколько сильно оно действует на стрелку, заставляя принять это направление.
Поля, подобно температуре не имеющие направления, называются скалярными. Они описываются одним числом: величиной. Скалярные поля играют важную роль в физике элементарных частиц. Согласно современным теориям, пространство Вселенной заполнено рядом скалярных полей, величины которых определяют энергию вакуума, а также массы частиц и их взаимодействия. Другими словами, эти поля задают вакуум, в котором мы живем. В настоящее время значения скалярных полей соответствуют истинному вакууму, но в прошлом они могли быть иными.
Чтобы проиллюстрировать физику распада вакуума, рассмотрим единственное скалярное поле и сконцентрируемся на том, как оно влияет на энергию вакуума. Каждый кубический сантиметр пространства содержит энергию, которая зависит от величины поля. Точный характер зависимости пока неизвестен, однако в общих чертах он напоминает холмистый ландшафт, как на рисунке 6.2, с максимумами на одних значениях и минимумами на других. Поведение скалярного поля очень похоже на поведение шарика, катящегося по поверхности с рельефом, подобным этому энергетическому ландшафту. В зависимости от начального положения шарик скатится в тот или иной энергетический минимум. Самый нижний минимум имеет почти нулевую плотность энергии; он отвечает истинному вакууму. Более высокий минимум соответствует высокоэнергичному ложному вакууму.
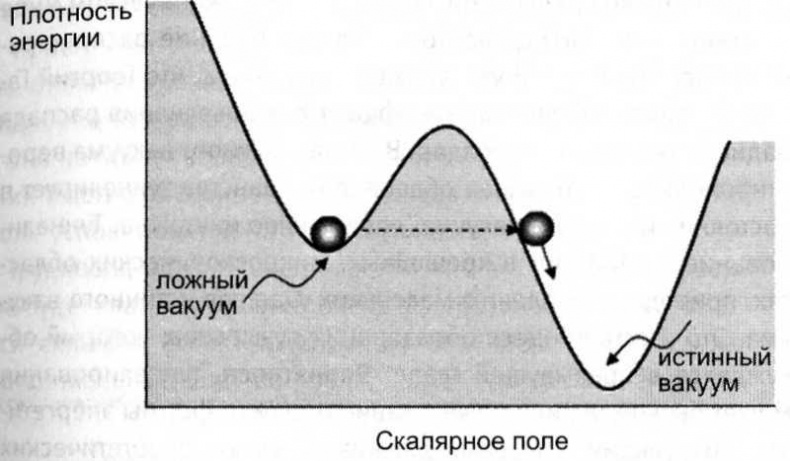
Рис. 6.2. Энергетический ландшафт скалярного поля с ложным и истинным вакуумом. Поле может туннелировать сквозь барьер, разделяющий два вакуума.
Допустим, мы начинаем с ложного вакуума во всех точках пространства. Это соответствует шарику, покоящемуся в верхнем минимуме. Он будет лежать там очень долго, пока что-нибудь не подтолкнет его вверх, сообщив энергию, необходимую для того, чтобы преодолеть барьер и попасть в нижний минимум. Однако, согласно квантовой теории, объект может "туннелировать" сквозь энергетический барьер. Когда вы наблюдаете такое событие, то видите, как шарик исчезает и мгновенно материализуется по другую сторону барьера.
Квантовое туннелирование — вероятностный процесс. Нельзя точно предсказать, когда оно произойдет, но можно вычислить вероятность, с которой оно случится в заданный отрезок времени. Для макроскопических объектов вроде шарика вероятность туннелирования чрезвычайно мала. Если, к примеру, вы хотите, чтобы банка колы туннелировала к вам из торгового автомата, время ожидания намного превысит современный возраст Вселенной. Однако в микроскопическом мире элементарных частиц квантовое туннелирование распространено гораздо шире. Я уже упоминал в главе 4, что Георгий Гамов использовал туннельный эффект для объяснения распада радиоактивных атомных ядер. В случае ложного вакуума вероятность того, что большая область пространства туннелирует в состояние истинного вакуума, совершенно ничтожна. Туннелирование происходит в крошечных, микроскопических областях, приводя к появлению маленьких участков истинного вакуума. Это и есть процесс образования пузырьков, который обсуждался в предыдущей главе. Вероятность туннелирования может быть выше или ниже в зависимости от формы энергетической функции. (Она выше для низких и узких энергетических барьеров.)
Несмотря на сходство между туннелированием шарика и скалярного поля, между ними есть важное различие. Мяч туннелирует между двумя разными точками в пространстве, тогда как скалярное поле — между различными значениями поля в одном и том же месте.




