При помощи этого метода Иоаннес ведет обратный учет, который помогает ему тянуть нить: когда он попадает в тупик, он может вернуться и пойти по другому пути.
[21] Возможность вернуться к месту пересечения ходов и попробовать более удачный путь гарантирует, что Иоаннес рано или поздно найдет дорогу обратно. Эта стратегия нахождения выхода из лабиринта называется алгоритм Тремо, ей мы обязаны французскому математику Эдуарду Лукасу и его книге «Математические рекреации», изданной в 1882 году.
Недавние исследования доказывают, что другие существа (например, муравьи) тоже могут использовать что-то типа метода обратного отслеживания для нахождения пути, если тропинка обрывается. Этот способ быстрее метода 1 и помогает выбраться из замкнутых петель в отличие от метода 2.
Заметьте, что эти три метода полезны, только когда главная цель – выбраться из лабиринта. Есть и другие способы поисков выхода, которые могут быть гораздо быстрее, однако при их применении требуется знать, как устроен лабиринт. Кроме того, методы, которые мы рассмотрели, не гарантируют нахождения самого короткого пути из лабиринта.
В мире есть десятки настоящих лабиринтов, некоторые простираются на многие мили, и там усвоенные нами уроки можно применить на практике. Но вышеперечисленные методы могут пригодиться и в других ситуациях. В более общем виде идея прохода от одной точки до другой в замкнутом пространстве, похожем на лабиринт, выглядит так. Это сеть или график как альтернативный способ описания лабиринта, где проходы – края, а пересечения – вершины, находятся в ядре многих приложений, которыми мы пользуемся и полагаемся на них каждый день. Приложение, которое знает, как соединены дороги – OpenStreetMap, например, – может подсказать кратчайший путь от вашего дома до пляжа. Веб-сайт, который знает, как связаны люди, места и вещи – скажем, Google’s Knowledge Grap, – дает лучшие результаты поиска: интернет-сайт, который знает, кто ваши друзья – Facebook или LinkedIn, например, – может догадаться, с кем еще вы знакомы, а программа, которая знает, как соединены ее компоненты и модули – скажем, Firefox, – предвидит, где вероятнее всего проявятся дефекты в будущем, основываясь на паттернах и плотности соединений.
Даже роботы-пылесосы служат хорошим примером. Не все они одинаковы. Уровень сложности зависит от того, как много пространства они способны охватить. Самые простые пылесосы бродят беспорядочными линиями или кругами, в то время как более продвинутые сначала составляют карту комнаты, определяя, где находятся стены, углы и повороты, а потом ездят взад-вперед по принципу решетки. Иными словами, когда робот знает, как лучше всего добраться с одного конца комнаты в другой, это приближает его цель, а результат – более чистая комната.
[22]
В случае с Иоаннисом он выберется из лабиринта и не сойдет с ума, независимо от того, каким методом воспользуется. Но если он продолжит бесконтрольно копить хлам, а его лавка будет и дальше разрастаться, то ему придется все время ходить по ней с клубком ниток в кармане.


5
Сортировка почты

Чарли Магна не успевает закончить свои почтовые дела. Сейчас уже середина дня, июль, Кейптаун. Температура 45 °C. К тому же рассеянный и неуклюжий Чарли выронил коробку с отсортированными письмами и перемешал пачки, которые нужно доставить 33 адресатам в его округе. Но и это не все: у почтальона повышенная чувствительность к солнечному свету, а он забыл кепку и солнцезащитные очки дома. Стоя на коленях на раскаленной гальке, он собирает конверты и пытается разложить их в нужном порядке, чтобы закончить работу, прежде чем на коже появятся волдыри.
Подсказка: подумайте, как можно разбить одну большую проблему на несколько маленьких.
Порядок поможет нам управиться с задачей быстрее. Представьте, что было бы, если бы местная газета не анонсировала предстоящие события по дням недели. Если бы серии телесериала, которые вы планируете посмотреть, не перечислялись в телепрограмме. Как было бы досадно тратить время на поиски следующего эпизода, вместо того чтобы посмотреть очередную историю о неудавшемся наркодилере, получившем еще один удар от жестокой вселенной.
Давайте посмотрим, как Чарли может справиться со своей неожиданной поблемой.
ЦЕЛЬ: СНОВА РАЗЛОЖИТЬ РАССЫПАННЫЕ ПАЧКИ КОНВЕРТОВ В НУЖНОМ ПОРЯДКЕ
МЕТОД 1: ПОЛОЖИТЬ ОДНУ ПАЧКУ НА ЗЕМЛЮ ПЕРЕД СОБОЙ. ВЗЯТЬ ВТОРУЮ ПАЧКУ, И, ЕСЛИ МЕСТО ЖИТЕЛЬСТВА АДРЕСАТА БЛИЗКО К ПЕРВОМУ, ПОМЕСТИТЬ ЕЕ СЛЕВА. И ТАК ДАЛЕЕ, ПОКА САМЫЕ БЛИЗКИЕ АДРЕСА НЕ ОКАЖУТСЯ СЛЕВА ОТ ЛИНИИ, А САМЫЕ ДАЛЕКИЕ – СПРАВА.
МЕТОД 2: РАЗЛОЖИТЕ ПАЧКИ КОНВЕРТОВ В РЯД ПЕРЕД СОБОЙ. РАЗДЕЛИТЕ ИХ ТАК, ЧТОБЫ СПРАВА И СЛЕВА ОКАЗАЛОСЬ ОДИНАКОВОЕ КОЛИЧЕСТВО КОНВЕРТОВ. ЗАТЕМ РАЗДЕЛИТЕ КАЖДУЮ ГРУППУ ПОПОЛАМ. КЛАДИТЕ БЛИЗКИЙ АДРЕС СЛЕВА, А ДАЛЕКИЙ – СПРАВА. ЗАТЕМ ДЕЛАЙТЕ ЭТО ДЛЯ КАЖДОЙ ПАРЫ ПАР И ТАК ДАЛЕЕ.
Вот как эти два метода выглядят на графике:
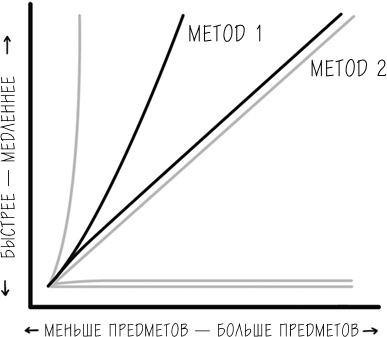
В реальной жизни при сортировке каких-либо вещей вручную, как это делает Чарли, допустимы некоторые вариации метода 1, которые он скорее всего использовал бы. Как мы видели из прежних сравнительных графиков, общее правило таково: для сортировки нескольких вещей годится любой метод. И только когда предметов много, один из методов может оказаться намного лучше другого. Хотя метод 2 не всегда имеет практическую корреляцию в реальной жизни, по крайней мере при сортировке, мы обсудим общий подход в концептуальных терминах.
[23]






