Если Кви не удастся выполнить задание в полном объеме, то какой результат будет для нее вторым по значимости? Если она решит уделять больше внимания высокоприоритетным задачам, то вдруг первое же задание, за которое она возьмется, займет целую неделю? Можно ли это совместить?
[37] Такие вопросы порой порождают творческие и оригинальные решения.
Отступление: в романе Кейго Хигашино «Страсть подозреваемого Х» (2005) учитель математики говорит о решении геометрической задачи путем превращения ее в алгебраическую, чтобы понять, как оценивают его студенты свои пробелы в знаниях. Это удивительное напоминание о том, насколько легко принимать прочитанное как данность, не оспаривая его. Мы интерпретируем новую информацию тем способом, который соответствует имеющимся у нас знаниям. Это явление ученый-компьютерщик Алан Кай назвал релятивизацией. Оно может стать и пороком, и добродетелью, в зависимости от того, как ее использовать.

9
Как починить ожерелье?

Джо – независимая ремесленница. Она продает свои поделки на рынке в Нью-Мехико, или на Индейском рынке, как его часто называют на рекламных плакатах. Много лет она страдает от ревматоидного артрита, поэтому ей все труднее зарабатывать на жизнь. Ее работа связана с ручным трудом: она изготавливает на заказ ожерелья с именами. Прилавок Джо расположен рядом со входом на рынок, и она убеждает каждого посетителя, что лучший подарок, который можно купить на рынке, это ожерелье с именем любимого человека или своим собственным.
Маленькая девочка поддалась на ее уговоры. «Меня зовут Жаклин», – говорит она. Джо приступает к работе, нанизывая бусины на простой кусок шпагата, к которому на концах приклеивается застежка. Она отдает законченную вещь девочке, но та мотает головой. Ей не нравится ожерелье. «Простите, но в моем имени две буквы «к». Разве вы не знали, что детям теперь модно давать оригинальные имена?» Бедная Джо!
В главе 1 мы говорили о массивах как о способе хранить группы элементов, которые могут быть быстро просмотрены в линейном времени. А в главе 3 мы узнали, что есть алгоритмы для выполнения заданий, на которые уходит постоянное количество времени независимо от величины задания. Сейчас мы поговорим об алгоритме, который концентрируется на возможности добавлять и удалять элементы в любых точках и за постоянное время. Для начала давайте рассмотрим два способа, при помощи которых Джо может исправить ожерелье Жаклин.
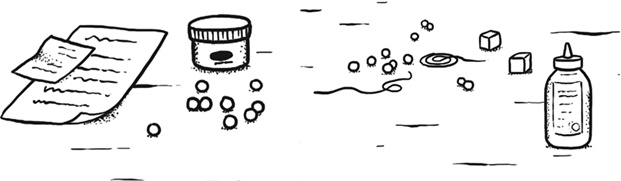
ЦЕЛЬ: ДОБАВИТЬ ШАРИК С ПРОПУЩЕННОЙ БУКВОЙ НА ОЖЕРЕЛЬЕ.
МЕТОД 1: РАССТЕГНУТЬ ОЖЕРЕЛЬЕ, УДАЛИТЬ ВСЕ БУСИНЫ, ПОКА НЕ ДОБЕРЕШЬСЯ ДО БУКВЫ «К» ИЛИ «Л». ДОБАВИТЬ ПРОПУЩЕННУЮ БУКВУ, НАНИЗАТЬ ОСТАЛЬНЫЕ БУСИНЫ.
МЕТОД 2: РАЗРЕЗАТЬ ОЖЕРЕЛЬЕ МЕЖДУ БУКВАМИ «К» И «Л». ВСТАВИТЬ БУКУ «К» НА ЛЮБОЙ ИЗ ОТРЕЗКОВ. СКРЕПИТЬ ШПАГАТ КЛЕЕМ.
У массивов есть недостатки – элементы, которые появляются рядом друг с другом, так же рядом и хранятся в памяти. Если возникает необходимость вставить новый элемент между двумя другими, мы не можем сделать это просто так: нам придется сдвинуть все элементы, расположенные после этой точки, чтобы освободить место для нового. Так поступают в соответствии с методом 1. Джо нужно по очереди удалить бусины с любого конца ожерелья, пока она не доберется до места, где должна стоять дополнительная бусина. Потом она нанизывает ее на шпагат и ставит на место все остальные. Процесс займет вдвое больше времени, если имя заказчика будет длиннее в два раза.
[38]
Новизна метода 2 состоит в том, что кусок шпагата может быть разрезан в любой точке и затем связан или склеен. Это важное свойство шпагата, потому что – и в этом мы сейчас убедимся – оно позволяет нам устранить главный недостаток массивов, в которых добавление или удаление элемента означает высокие трудозатраты. До определенного момента метод 1 может оказаться лучшим: чего стоит удаление одной-двух бусин по сравнению с разрезанием шпагата и связыванием двух концов? Но вряд ли его преимущество сохранится, если в ожерелье окажется больше бусин.
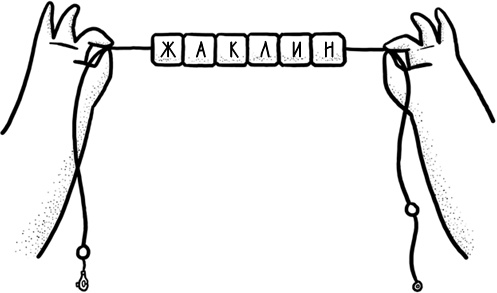
В информатике существует структура, которая проявляет именно это свойство, и вот как она выглядит:
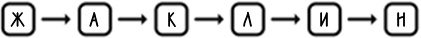
У нас есть группа элементов, но мы больше не ограничены необходимостью хранить их рядом друг с другом. Вместо этого каждый элемент в группе просто указывает на другой, стоящий рядом с ним. Эта связь, или же ссылкамежду каждой парой элементов, очень похожа на шпагат Джо. И теперь, если мы хотим добавить элемент, нам не нужно больше освобождать для него место. Мы можем просто видоизменить соответствующие ссылки. То же самое относится и к удалению элементов.
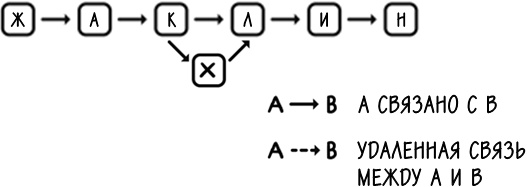
Эта структура, разработанная еще в 50-е годы, известна под названием связный список. Она стала основой для многих приложений в вычислительной технике из-за ее эффективности при вставке и удалении элементов из группы в заданной точке. Например, в главе 8 мы упомянули, что принтер может ставить задания в очередь, хранить их в списке и решать, поместить ли менее объемные задания перед другими. Эффективным способом для этого будет создание очереди с использованием связного списка.