ЦЕЛЬ: СОЧИНИТЬ ОСТРОУМНУЮ ФРАЗУ-СТАТУС, КОТОРАЯ СОДЕРЖИТ НЕ БОЛЬШЕ 140 СИМВОЛОВ.
МЕТОД 1: ЗАМЕНЯТЬ ДЛИННЫЕ СЛОВА НА КОРОТКИЕ, НО МЕНЕЕ ТОЧНЫЕ.
МЕТОД 2: ОПУСКАТЬ ЧАСТО ВСТРЕЧАЮЩИЕСЯ БУКВЫ, НАПРИМЕР ГЛАСНЫЕ, В НЕКОТОРЫХ СЛОВАХ.
Поразительно, но у метода 2 есть аналог в информационных технологиях. В 1952 году ученый Дэвид А. Хаффман изобрел способ сокращения пространства, необходимого для хранения данных. В отличие от прежних методов алгоритм Хаффмана не требовал удаления информации, а концентрировался на оптимизации.
Компьютеры хранят словесную информацию, кодируя буквы алфавита, цифры и другие символы и занося их в таблицу, где им присваиваются числовые значения. Эти значения затем сохраняются в том виде, какой понимает компьютер, – он называется бинарным, или двоичным, кодом. Каждый символ в нем представлен в виде кода, который может состоять из семи бит. Например, буква «а» английского алфавита имеет значение 97, а в двоичном коде запись этого числа выглядит так:
1100001
Буква «b» имеет значение 98 и в двоичном коде она такая:
Если бы нам нужно было представить слово «hans» в двоичном коде, то оно бы выглядело так (каждая буква занимает 7 бит, всего 28 бит):
1101000 1100001 1101110 1110011
То обстоятельство, что символы имеют двойные коды одинаковой длины (в нашем случае 7 бит), позволяет легко декодировать бинарную цепочку. Все, что нам нужно сделать, – считывать каждые семь бит и затем, используя таблицу соответствий, перекодировать их в слова английского языка.
Но Хаффман был хитер. Он посмотрел на эти семь бит и сказал: «Конечно, должен быть способ сжимать данные». Друзья отговаривали его. «Нет, Хаффман, – говорили они. – Этого нельзя сделать. Ты слишком многого хочешь. Не рвись в герои». Но Хаффман не слушал их. Он был готов броситься с головой в неизвестность, чтобы изобрести другое бинарное представление набора символов.

Вместо использования бинарных кодов с фиксированной длиной Хаффман стал применять бинарные коды разной длины. Он опирался на факт, что некоторые символы встречаются в письменной речи чаще, чем другие, поэтому он присвоил этим часто встречающимся буквам меньшие величины. Соответственно они имели более короткий бинарный код, а реже встречающиеся символы – более длинный.
Например, для нашего набора данных частота встречаемости символов распределяется так, как показано на таблице слева.
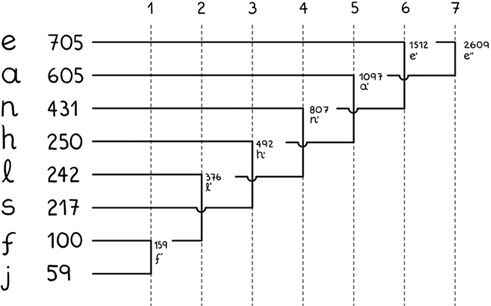
Буква «е» встречается нам 705 раз, буква «а» – 605 раз и так далее. Заметьте, что символы отсортированы сверху вниз в порядке убывания частоты. Согласно подходу Хаффмана, нужно взять пару символов с наименьшей частотой встречаемости, сложить их значения, сохраняя результат в новом вре́менном символе, а затем отсортировать набор. Процесс повторяется, пока у нас больше не останется пар символов.
В конечном итоге получается дерево, где каждый узел (символ) соединен с парой узлов, на основе которых он образовался, с двумя краями. Если мы произведем такую операцию с приведенным выше набором данных, то в конечном итоге получим что-то вроде схемы, где мы сначала соединяли «f» и «j», затем результат этого действия совмещали с «l» и так далее. Каждая колонка, начиная со второй, представляет собой один шаг алгоритма.
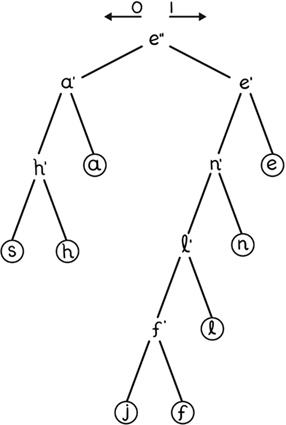
Когда мы преобразуем схему в дерево, все становится яснее. Оптимизированный двоичный код символа – это цепочка, которую мы получаем, считывая биты с самого верхнего, или корневого,
[31] узла и двигаясь ниже к узлу символа. Каждый раз, когда мы двигаем дерево влево, мы прибавляем ноль к двоичному коду символа, а при движении вправо добавляем единицу. Поэтому буква «е» заканчивается двухбитным двоичным кодом 11, а буква «f» представляет собой пятибитный код 10001. Приписывание 1 или 0 к дочернему узлу дерева Хаффмана производится факультативно, то есть литера «е» может быть закодирована как «01», а не как 11. Несмотря на то что двоичные коды не всегда уникальны, они считаются наиболее оптимальными. В любом случае дерево Хаффмана отсылается адресату вместе с сообщением, чтобы получатель знал, как его раскодировать.
Вот список оптимизированных двоичных кодов. Заметьте, что самые частые буквы имеют наиболее короткие коды.

Как же будет выглядеть слово «hans» в двоичном коде?
001 01 101 000
Для такой записи нам понадобилось 11 бит, а не 28. Это открытие заставляет вспомнить историю почти столетней давности о том, как передавали сообщения по телеграфу. Способ Самюэля Морзе кодировать буквы также был основан на том, насколько часто эти буквы встречались в английском языке. Морзе определял частоту различных букв не в ходе бесед с учеными или анализа данных – он просто считал литеры в шрифтовой каретке наборщика в типографии. Так что в следующий раз, когда какой-нибудь умник начнет критиковать ваши методы исследования, не отступайте.
Техники компрессии данных, подобные кодированию методом Хаффмана, чрезвычайно важны в современном мире. Оптимальное использование пространства означает, что вебсайты будут загружаться быстрее, веб-серверы могут сжимать файлы, прежде чем рассылать их по сети, а современные браузеры сумеют легко распаковывать их. Если место ограниченно, любое увеличение скорости имеет значение.
Компрессия также означает, что фильмы (то есть файлы формата MPEG-2), изображения (файлы формата JPEG) и песни (файлы формата МРЗ) могут занимать меньше пространства, что позволит сэкономить деньги на их хранении и пересылке. Аудиофайлы типа МРЗ интересны в том плане, что их сжатие основано на удалении того диапазона аудиосигналов, который человеческое ухо не может услышать из-за особенностей своего анатомического строения. Например, оно не воспринимает частоту свыше 20 000 Гц.






