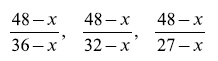— Цена на арбузы, я вижу, падает, — сказал он. — У вас остался всего один последний арбуз. Что вы хотите за него?
— 48 копеек, — ответил торговец.
— Вот так раз! — с досадой воскликнул милиционер. — Почему это вы берете с меня дороже, чем со всех других?
— Я ни с кого не беру лишнего, — ответил торговец. — На всем базаре не найдете более добросовестного торговца. Для меня все покупатели равны, такое уж у меня правило. Хочу со всех нажить одинаково, много ли покупают или мало.
Сколько арбузов было у торговца?
7
Учительница задала двум ученицам один и тот же пример на умножение:
1 год 1 мес. 11/4 дня × 36.
Первая девочка умножила сначала на 9, а полученное произведение — на 4. Ответ получился правильный.
Вторая девочка умножила сначала на 4, а потом на 9 и тоже получила правильный ответ.
Учительница оценила обе работы одинаково. Если предполагать, что вторая девочка избрала свой путь решения вполне сознательно, то учительница поступила несправедливо, дав обоим ответам одинаковую оценку. Почему?
Добавление редактора Решения задач
1) После того как мать взяла половину, осталась 1/2, после заимствования старшего брата осталась 1/4, после отца 1/8, после сестры 1/8 × 3/5 = 3/40. Если 30 сантиметров составляет 3/40 первоначальной длины, то искомая длина равна 30:3/40 = 400 сантиметрам, или 4 метрам.
2) Пусть часы пробили х. Наличное число очков надо обозначить через 2х. Если их было вдвое больше, т. е. 4х, то это число превышало бы втрое число ударов часов при последующем бое, т. е. (х + 1). Следовательно, имеем уравнение 4x/3 = x + 1, откуда x = 3. Было 3 часа.
3) Обозначим число наличных стульев через х. Тогда число учеников можно выразить двояко: через 3 (х + 5) и через 4 (х — 3). Оба выражения должны быть равны, откуда имеем уравнение
3 (x + 5) = 4 (x — 3).
Решив его, находим x = 27. Следовательно, стульев было 27, а учеников 3 × (27 + 5) = 96.
4) Обозначим расстояние между домами через х. Молодой человек всего прошел 2х, а доктор вчетверо меньше, т. е. x/2—. До встречи доктор прошел половину пройденного им пути, т. е. x/4, а молодой человек — остальное, т. е. 3x/4. Свою часть пути доктор прошел в x/12 часов, а молодой человек — в 3x/16 часов, причем мы знаем, что он был в пути на 3/4 часа дольше, чем доктор. Имеем уравнение:
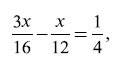
откуда × = 2,4 километра. Итак, от дома молодого человека до дома доктора — 2,4 километра.
5) Налив 300 граммов воды в чашку весов, отвешиваем этой «водяной гирей» сначала 300 граммов чаю. Затем, положив на одну чашку весов эти 300 граммов чаю, кладем на другую — пряжку, т. е. 650 граммов, и досыпаем на менее нагруженную чашу в отдельный пакет столько чаю, чтобы весы пришли в равновесие, — т. е. 350 г. Отвесив еще с помощью пряжки 650 г чаю, имеем 650 г + 350 г = 1000 г, т. е. 1 килограмм.
6) Обозначим себестоимость одного арбуза через х. Тогда чистая прибыль от продажи одного арбуза первой партии равна 36 — х, второй 32 — х, третьей 27 — х, наконец, последнего арбуза 48 — х. Так как чистая прибыль от продажи каждой партии одинакова, то число арбузов в первой партии должно равняться
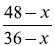 , во второй
, во второй
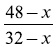 , в третьей
, в третьей
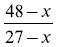 .
.
Все эти выражения, согласно условию задачи, суть целые числа. Надо, следовательно, подобрать для × такое значение, при котором выражения
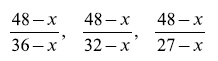
превращаются в целые числа. Нетрудно найти, путем нескольких испытаний, что этому условию удовлетворяет только × = 24. Тогда первое выражение равно 2, второе — 3, третье — 8. Другими словами, в первой партии было 2 арбуза, во второй 3, в третьей 8. Всего же арбузов было привезено торговцем 2 + 3 + 8 + 1 = 14.
7) Способ второй ученицы удобнее, так как при умножении 1 года 1 мес. 1 1/4 дней на 4 — мы сразу освобождаемся от дроби, и тогда умножение на 9 выполняется легче. Способ первой ученицы таких удобств не дает, он более громоздкий. Поэтому учительница должна была дать второму решению более высокую оценку.
Хитрое разрешение мудреной задачи
В. Г. Бенедиктов
[39]Одна баба, торговавшая яйцами, имея у себя к продаже девять десятков яиц, отправила на рынок трех дочерей своих и, вверив старшей и самой смышленой из них десяток, поручила другой 3 десятка, а третьей полсотни. При этом она сказала им:
— Условьтесь наперед между собой насчет цены, по которой вы продавать будете, и от этого условия не отступайтесь; все вы крепко держитесь одной и той же цены; но я надеюсь, что старшая дочь моя, по своей смышлености, даже и при общем между вами условии, по какой цене продавать, сумеет выручить столько за свой десяток, сколько вторая выручит за 3 десятка, да научит вторую сестру выручить за ее 3 десятка столько же, сколько младшая выручит за полсотни. Пусть выручки всех троих да цены будут одинаковы. Притом я желала бы, чтоб вы продали все яйца так, чтобы пришлось круглым счетом не меньше 10 копеек за десяток, а за все 9 десятков — не меньше 90 копеек, или 30-ти алтын.
Задача была мудреная. Дочери, идучи на рынок, стали между собой совещаться, причем вторая и третья обращались к уму и совету старшей. Та, обдумав дело, сказала:
— Будем, сестры, продавать наши яйца не десятками, как это делалось у нас до сих пор, а семерками: семь яиц — семерик; на каждый семерик и цену положим одну, которой все и будут крепко держаться, как мать сказала. Чур, не опускать с положенной цены ни копейки. За первый семерик алтын, согласны?



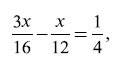
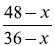 , во второй
, во второй
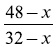 , в третьей
, в третьей
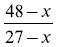 .
.