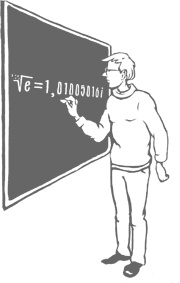
86. Считаем в уме III
В уме возвести 2 в 18-ю степень. Это:
Варианты ответов
1. 256 256.
2. 258 724.
3. 262 144.
Правильный ответ: 3
Любой программист (а нынче и простой пользователь электронных гаджетов, который, например, изучал надписи на карте памяти и узнал, что 1 Гб – это вовсе не 1000 Мб, а 1024) знает, сколько будет 210 – чуть больше тысячи, точнее, те самые 1024. А 220 – соответственно 1024 × 1024. Но как это поможет вычислить 218? Очень просто: 218 = 220 ∕ 22 = 1024 × 1024 ∕ 2 × 2 = 512 × 512. А это уже совсем просто посчитать, вспомнив, что (a + b) × (a + b) = a² + 2ab + b² (сравните с задачей № 41). Применительно к нашему примеру (500 + 12) × (500 + 12) = 500² + 2 × 12 × 500 + 12² = 250 000 + 12 000 + 144 = 262 144.
87. Считаем в уме IV
Что больше – десять в пятой степени или пять в десятой?
Варианты ответов
1. 105 > 510.
2. 510 > 105.
3. Возможно, они равны?
Правильный ответ: 2
Сколько будет 105, мы, конечно же, знаем – это единица с пятью нулями, 100 000. А 510? На самом деле, вооружившись знаниями из предыдущего примера (№ 43), мы тоже легко можем посчитать, хотя бы приблизительно. Заметив, что 5 = 10/2, возведем последнюю дробь в десятую степень, помня правило возведения дроби в степень (числитель и знаменатель можно возводить в нее порознь), получим 1010/210, а поскольку 210, как мы теперь уже знаем, это примерно 1000, т. е. 10³, получаем 510 ≈ 1010/103 = 107 = 10 000 000. Значит, пять в десятой степени почти в 100 раз больше, чем десять в пятой! Интересно решить более общую задачу: если m > n, всегда ли, как в этом случае, nm больше, чем mn? Оказывается, если и m, и n больше двойки (3, 4, 5 и т. д.), то да, всегда. А вот когда n = 2, есть два интересных случая: когда m = 3, 2³ (8) меньше, чем 3² (9), а когда m = 4, то 24 и 42 и вовсе равны (это 16). Если же m равно 5, 6 и т. д., мы снова возвращаемся к общему правилу 2m > m².
88. Братья и сестры
У Саши сестер на двое больше, чем братьев. На сколько у Сашиных родителей больше дочерей, чем сыновей?
Варианты ответов
1. На одну.
2. На три.
3. Невозможно определить.
Правильный ответ: 3
Предположим для простоты, что у Саши две сестры и вовсе нет братьев. Тогда дочерей у Сашиных родителей на три больше, чем сыновей, если Саша девочка, и на одну, если он мальчик. Поскольку Саша – имя универсальное, может быть как мужским, так и женским, пол Саши определить не представляется возможным, как и ответить на поставленный в задаче вопрос.

Физика
89. Льдина в бассейне
В бассейне плавает глыба льда. Через некоторое время она тает. Что случилось с уровнем воды в бассейне?
Варианты ответов
1. Повысился.
2. Понизился.
3. Остался неизменным.
Правильный ответ: 3
Уровень воды, разумеется, не изменится, и это очень легко объяснить наглядно. Поместим льдину в бесконечно легкую кастрюлю и пустим плавать в нашем бассейне. Льдина растаяла, но, так как масса содержимого кастрюли не изменилась, не изменился и уровень воды в бассейне. При этом, очевидно, уровень воды внутри (после таяния льда) и снаружи кастрюли (раз она не имеет массы) обязаны совпадать. Мысленно удаляем нашу воображаемую кастрюлю – вуаля, наше предположение доказано. Привет сторонникам теории глобального потепления.

90. Без весла
Посреди озера в штиль рыбак умудрился сломать весло. Рыбак подумал, что сможет плыть и без весла, если будет действовать следующим образом: бегом бежать от кормы к носу лодки и медленным шагом возвращаться обратно. Прав ли рыбак и в какую сторону он в таком случае поплывет?
Варианты ответов
1. Разрази его гром, прав! Поплывет носом вперед.
2. Прав, морской черт! Только поплывет он задом – кормой вперед.
3. Дурак ваш рыбак, и метод его дурацкий.
Правильный ответ: 1
Если представить, что трения об воду нет, то рыбацкий труд, конечно, не имел бы смысла: по закону сохранения импульса лодка смещалась бы против направления движения рыбака, а за полный цикл (корма – нос – корма) смещение равнялось бы нулю. Но трение в воде есть, более того, оно квадратично зависит от скорости: чем больше скорость (лодки), тем сильнее сопротивление воды. Соответственно, когда рыбак бежит от кормы к носу, лодка смещается назад на меньшее расстояние, чем вперед – когда он неспешно прогуливается в обратном направлении.

91. Камни на пашне
Каждый год по весне на пахотных землях появляются камни, про такие говорят, что они «из земли растут». Откуда они берутся?
Варианты ответов

