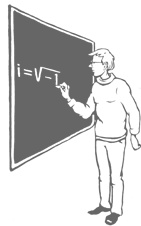
67. Делиться надо
Нужно найти все натуральные числа от 1 до 1000, делящиеся одновременно на 7 и на 11. Сколько таких?
Варианты ответов
1. 7.
2. 10.
3. 12.
Правильный ответ: 3
Поскольку 7 и 11 – простые числа, то понятно: для того чтобы число делилось и на 7, и на 11, нужно, чтобы оно делилось на 77. Итоговое произведение этих чисел (1 × 77, 2 × 77, … – и так вплоть до n × 77) не должно превышать 1000. При n = 12 это 924, а при n = 13 уже 1001, не подходит. Так что правильный ответ – 12.
68. Который час?
Когда в Москве 12:00, в Чикаго 3:00. Когда же 3:00 в Москве, 12:00 в Петропавловске-Камчатском. А который час в Чикаго, когда в Петропавловске-Камчатском 3:00?
Варианты ответов
1. 12:00.
2. 21:00.
3. 9:00.
Правильный ответ: 3
В Москве по отношению к Чикаго +9 часов, в Петропавловске-Камчатском по отношению к Москве +9 часов, соответственно, в Чикаго по отношению к Петропавловску-Камчатскому – 18 часов, там всегда на 18 часов меньше, чем в нашем дальневосточном городе. Значит, когда в Петропавловске-Камчатском 3:00, в Чикаго −15 – т. е. 24−15 = 9, 9:00 предыдущего дня.
69. Средний возраст
В отделе продаж фирмы работают молодые люди: девять красавцев средним возрастом 25 лет. А в бухгалтерии – без пяти минут пенсионеры, 11 счетоводов, им в среднем по 45. А что можно сказать про средний возраст персонала фирмы? (Предположим для простоты, что более никаких отделов в компании нет.)
Варианты ответов
1. 35 лет.
2. 36 лет.
3. 38 лет.
Правильный ответ: 2
Элементарная задачка, если вспомнить определение среднего. Средний возраст равен сумме всех возрастов (суммарный возраст), деленной на число людей. Значит, нам нужно посчитать сначала суммарный возраст всех сотрудников, который равен {суммарный возраст по отделу продаж} + {суммарный возраст по бухгалтерии} = 25 × 9 + 45 × 11 = 720 лет. Теперь, чтобы получить средний возраст, делим найденный суммарный на общее число сотрудников (9 + 11 = 20), получаем 36 лет.

70. Сколько чисел?
Среди всех трехзначных чисел есть такие, сумма цифр которых ровно в 12 раз меньше самого числа. Сколько таких?
Варианты ответов
1. Только одно.
2. Два.
3. Шесть.
Правильный ответ: 1
Любое трехзначное число можно записать как 100a + 10b + c, где a, b и c принимают целочисленные значения (уже пятая диофантова задача! См. № 47, 55, 62 и 64), b и c в диапазоне от 0 до 9, a – от 1 до 9. По условию само число равно сумме цифр, умноженной на 12: 100a + 10b + c = 12 (a + b + c). Упрощая, запишем: 88a = 2b + 11c, a = (2b + 11c) ∕ 88a = 1 при 2b + 11c = 88, при этом значение a = 2, не говоря уж о бóльших, невозможно – тогда 2b + 11c должно сравняться со 176, для b и c меньших 9 это просто немыслимо. В общем, a всегда единица, c = 8 при b = 0, а больше никаких возможностей не существует: можно взять еще c = 6, но тогда b = 11, снова вышли за пределы допустимого диапазона. Выходит, единственное число, удовлетворяющее условию, – это 108 = 12 × 9.

71. Специалист
Профессионал выполняет работу за 5 ч, стажер за 10 ч. А за какое время справится специалист, производительность которого – среднее арифметическое от производительности профессионала и стажера?
Варианты ответов
1. За 6 ч 40 м.
2. За 7 ч 30 м.
3. За 8 ч 20 м.
Правильный ответ: 1
Ответ «семь с половиной часов» – типичная ошибка, связанная с тем, что прежде, чем усреднять, нужно определиться, что именно мы усредняем. В задаче речь о производительности, давайте ее посчитаем. Производительность – это работа в единицу времени. Если принять ту работу, о которой говорится в условии, за единицу, то производительность профи 1/5, стажера 1/10, специалиста – (1/5 + 1/10)/2 = 3/20, а работу единичного объема он выполнит за 20/3 ч = 6 ч 40 м.
72. Как отмерить?
В вашем распоряжении две банки – трех– и пятилитровая. Нужно отмерить ровно 1 л воды. Возможно ли это, и если да, то за сколько шагов (шаг = одно наливание из крана или одно переливание из одной банки в другую)?
Варианты ответов
1. Невозможно.
2. За четыре шага.
3. За восемь шагов.
Правильный ответ: 2
Чтобы понять, как действовать, сначала нужно прикинуть, как из 3 и 5 получить 1, чисто арифметически. Самый простой вариант: 1 = 3 + 3–5, т. е. нам нужно как-то дважды налить по 3 л, а после куда-то деть 5 л. Возможно? Возможно: наполняем трехлитровую банку (1-й шаг) и переливаем все ее содержимое в пятилитровую (2-й шаг), затем снова наполняем трехлитровую (3-й шаг) и снова переливаем в пятилитровую (4-й шаг) – в нее войдет только 2 л, после чего в трехлитровой банке останется ровно 1 л воды.

