1 кг = 1, 2 кг = 2, 3 кг = 2 + 1, 4 кг = 4, …, 5 кг = 4 + 1, …, 40 кг = 32 + 8.
Но грузы можно взвешивать и по-другому, а именно: располагая гири на обеих чашах весов, т. е. не только на чаше, свободной в начале взвешивания, но и на чаше с грузом. При таком способе взвешивания Баше понадобились только 4 гири: 1, 3, 9 и 27 кг. Гиря, помещаемая на одну чашу с грузом, как бы приобретает отрицательный вес. Способ Баше позволяет взвесить любой груз от 1 до 40 кг, ставя гири на обе чаши весов в следующих комбинациях:
1 кг = 1, 2 кг = 3–1, 3 кг = 3, 4 кг = 3 + 1, 5 кг = 9–3 — 1, …, 40 кг = 27 + 9 + 3 + 1.
Приложение 5. Доказательство Евклида существования бесконечного числа пифагоровых троек
Пифагоровой тройкой называется такой набор из трех целых чисел, что сумма квадратов двух из них равна квадрату третьего числа. Евклид сумел доказать, что существует бесконечно много таких пифагоровых троек.
Предложенное Евклидом доказательство начинается с наблюдения: разность квадратов последовательных целых чисел всегда равна какому-нибудь нечетному числу:

Прибавив каждое из бесконечного множества нечетных чисел к соответствующему квадрату, мы получим другой квадрат. Некоторые нечетные числа, составляющие часть всех нечетных чисел, сами являются квадратами (например, 32, 52, 72 и т. д.). Следовательно, существует бесконечно много нечетных квадратов, которые можно прибавить к квадрату и получить другой квадрат. Иначе говоря, существует бесконечно много пифагоровых троек.
Приложение 6. Доказательство гипотезы о трех точках
Гипотеза о трех точках утверждает, что невозможно построить точную диаграмму так, чтобы на каждой прямой было по крайней мере три точки. Хотя это доказательство требует минимальных познаний в математике, оно опирается на некоторую геометрическую «гимнастику», и поэтому следует тщательно продумать каждый его шаг.
Начнем с произвольно расположенных точек. Проведем через каждую точку прямые, соединяющие ее со всеми остальными точками. Затем для каждой точки измерим расстояние, отделяющие ее от ближайшей прямой, и найдем ту из точек, которая ближе, чем все остальные, находится от некоторой прямой.
На рисунке внизу изображена такая точка D, которую от прямой L отделяет самое короткое расстояние. На рисунке это расстояние показано штриховой линией. Оно короче, чем расстояние, отделяющее любую другую точку от ближайшей к ней линии. Теперь можно показать, что на прямой L всегда лежат только две точки и что, следовательно, гипотеза верна, т. е. невозможно построить точечную диаграмму так, чтобы на каждой прямой лежали три точки.
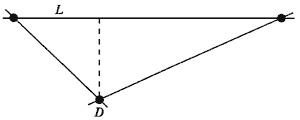
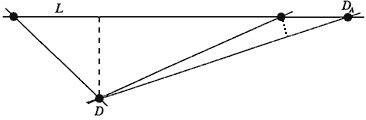
Чтобы показать, что на прямой L должны лежать две точки, рассмотрим, что случилось бы, если бы на ней оказалось третья точка. Если бы третья точка DA лежала на прямой L вне двух точек, через которые она проходит, то расстояние, показанное пунктирной линией, было бы короче расстояния, показанного штриховой линией. Между тем это расстояние по предположению, наименьшее из всех кратчайших расстояний, отделяющих точку диаграммы от линии. Следовательно, точка DA существовать не может.
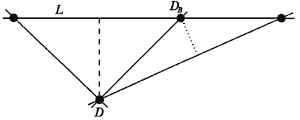
Аналогично, если бы третья точка DB оказалась на прямой между двумя точками, то расстояние, показанное пунктиром, оказалось бы короче расстояния, показанного штрихом, по предположению наименьшего из кратчайших расстояний от точки диаграммы до прямой.
Следовательно, для каждой конфигурации всегда существует по крайней мере эта прямая, которой принадлежат только две точки диаграммы, и гипотеза верна.
Приложение 7. Пример неправильного доказательства
Приведем классический пример того, как легко, начав с очень простого утверждения и сделав всего лишь несколько, казалось бы, прямых и вполне логичных шагов, показать, 2=1.
Начнем с невинного утверждения о том, что
a = b.
Умножив обе части равенства на a, получим:
a2 = ab.
Добавив к обеим частям равенства по a2–2ab:
a2 + a2 – 2ab = ab + a2 – 2ab.
Это равенство можно упростить:
2(a2 — ab) = a2 — ab.
Наконец, сокращая это выражение на a2-ab получаем требуемое равенство 2=1.
Исходное утверждение казалось совершенно безвредным (и на самом деле оно не таит в себе ничего плохого), но, производя шаг за шагом преобразования равенства a=b, мы допустили маленькую, но роковую ошибку, которая и привела нас к противоречию. Эту ошибку мы допустили, производя последнее преобразование, когда разделили обе части равенства на a2-ab. Из исходного утверждения нам известно, что a=b. Следовательно, деление на a2-ab эквивалентно делению на нуль.
Такого рода тонкая ошибка типична для просчетов, допущенных многими соискателями премии Вольфскеля.
Приложение 8. Аксиомы арифметики
Величественное здание арифметики опирается на следующие аксиомы.
1. Для любых чисел m и n
m + n = n + m и mn = nm.
2. Для любых чисел m, n и k
(m + n) + k = m + (n + k) и (mn)k = m(nk).
3. Для любых чисел m, n и k
m(n + k) = mn + mk.
4. Существует число 0, такое, что для любого числа n
n + 0 = n.
5. Существует число 1, такое, что для любого числа n
n·1 = n.
6. Для любого числа n существует другое число k, такое, что
n + k = 0.
7. Для любых чисел m, n и k
если k ≠ 0 и kn = km, то m = n.

