Приложения
Приложение 1. Доказательство теоремы Пифагора
Цель доказательства — убедиться в том, что теорема Пифагора верна для всех прямоугольных треугольников. Треугольник, изображенный на рисунке слева, может быть любым прямоугольным треугольником, так как длины его сторон не указаны, а обозначены буквами x, y и z. Справа из четырех одинаковых прямоугольных треугольников и наклоненного квадрата составлен квадрат больших размеров. Площадь большего квадрата — ключ к доказательству.
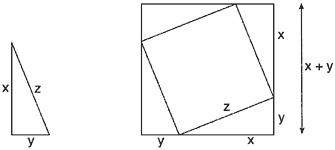
Площадь большого квадрата можно вычислить двумя способами.
1-й способ. Измеряем площадь большого квадрата как единой фигуры. Длина каждой стороны равна x+y. Следовательно, площадь большого квадрата равна (x+y)2.
2-й способ. Измеряем площадь каждого элемента большого квадрата. Площадь каждого треугольника равна xy/2. Площадь наклонного квадрата равна z2. Следовательно, площадь большого квадрата равна 4 × (площадь каждого треугольника) + (площадь наклонного квадрата) = 4·xy/2 + z2. 1-й и 2-й способы приводят к двум различным выражениям. Оба выражения должны быть равны, так как они представляют различные записи одной и той же площади. Следовательно,
(x + y)2 = 4·xy/2 + z2.
Раскроем скобки и упростим полученные выражения:
x2 + 2xy + y2 = 2xy + z2.
Члены 2xy, стоящие в левой и правой частях равенства, взаимно уничтожаются, и мы получаем
x2 + y2 = z2.
Это и есть теорема Пифагора!
Приведенное доказательство остается в силе для любых прямоугольных треугольников. Длины сторон треугольника в нашем доказательстве обозначены буквами x, y и z, которые могут быть длинами сторон любого прямоугольного треугольника.
Приложение 2. Доказательство Евклида иррациональности числа √2
Цель Евклида состояла в доказательстве того, что число √2 не представимо в виде дроби. Поскольку Евклид использовал доказательство от противного, первый шаг состоял в предположении, что верно противоположное утверждение, т. е. что число √2 представимо в виде некоторой неизвестной дроби. Запишем эту дробь в виде p/q, где p и q — два целых числа.
Прежде чем приступать к самому доказательству, необходимо напомнить некоторые основные свойства дробей и четных чисел.
1) Если взять любое число и умножить его на 2, то произведение должно быть четным. По существу, это определение четного числа.
2) Если квадрат некоторого числа четен, то и само число должно быть четным.
3) Наконец, дроби можно сокращать: 16/24 это то же самое число, что и 8/12. Чтобы убедиться в этом разделите числитель и знаменатель дроби 16/24 на общий множитель 2. Кроме того, число 8/12 это же самое, что и 4/6, а 4/6 это же самое, что и 2/3. Дробь 2/3 не подлежит дальнейшему сокращению, так как 2 и 3 не имеют общих множителей. Дробь невозможно сокращать до бесконечности.
Напомним, что по мнению Евклида число √2 не представимо в виде дроби. Но поскольку Евклид использовал доказательство от противного, он начал с предположения, что дробь p/q, равная числу √2, существует, а затем исследовал, к каким последствиям приводит такое предположение:
√2 = p/q.
Возводя обе части равенства в квадрат, получаем
2 = p2/q2.
После несложного преобразования запишем это равенство в виде
2q2 = p2.
Из 1) мы знаем, что число p2 должно быть четным. Кроме того, из 2) нам известно, что число p также должно быть четным. Но если p четно, то, как следует из 1), его можно записать в виде 2m, где m — некоторое другое целое число. Подставляя p = 2m в равенство для p2, получаем
2q2 = (2m)2 = 4m2.
Сокращаем правую и левую части равенства на 2:
q2 = 2m2.
Рассуждая так же, как прежде, заключаем, что число q2 должно быть четным. Значит, и само число q должно быть четным. Но если это так, то q можно записать в виде q = 2n, где n — некоторое другое целое число. Возвращаясь к исходной записи числа √2, получаем:
√2 = p/q = 2m/2n.
Дробь 2m/2n можно сократить, разделив числитель и знаменатель на 2:
√2 = m/n.
Мы получаем дробь m/n, которая проще, чем p/q (имеет меньший числитель и знаменатель). Теперь мы как бы снова оказались находимся на исходной позиции, и, проделав с дробью m/n все, что мы проделали с дробью p/qn, получим в результате еще более простую дробь, например, g/h. Проделав с этой дробью тоже самое, приведем ее к еще более простой дроби t/f, и т. д. Аналогичную процедуру можно проделывать бесконечное число раз. Но из 3) мы знаем, что дробь невозможно упрощать бесконечно — всегда существует простейшая дробь. Но наша исходная гипотетическая дробь p/q, насколько можно судить, не подчиняется этому правилу. Следовательно мы получили противоречие. Итак, мы можем утверждать, что число √2 не представимо в виде дроби, а это означает оно является иррациональным числом.
Приложение 3. Загадка о возрасте Диофанта
Обозначим продолжительность жизни Диофанта через L. Из загадки нам известно, как протекала жизнь Диофанта: 1/6 жизни, т. е. L/6, пришлась на его детство; L/12 — на юношеские годы; L/7 прошла прежде, чем он женился; через 5 лет у него родился сын; сын прожил L/2 жизни отца; 4 года Диофант оплакивал смерть сына прежде, чем умер.
Таким образом, продолжительность жизни Диофанта L можно записать в виде суммы:
L = L/6 + L/12 + L/7 + 5 + L/2 + 4.
Отсюда L = 84. Итак, Диофант умер в возрасте 84 лет.
Приложение 4. Задача Баше о наборе гирь
Чтобы взвесить любое целое число килограммов от 1 до 40, по мнению большинства людей необходимо иметь 6 гирь: 1, 2, 4, 8, 16 и 32 кг. Действительно, такой набор гирь позволяет взвесить любой груз от 1 до 40 кг, помещая его на одну чашу весов и ставя на другую следующие комбинации гирь:

