Эти факты служат иллюстрацией ситуации, которая верна в общем случае. Всякая (N×N)-матрица имеет характеристический многочлен степени N, и этот многочлен имеет N нулей.
[163] Нули характеристического многочлена матрицы невероятно важны. Они называются собственными значениями матрицы. Заметим еще одно. Если сложить числа на главной диагонали нашей (2×2)-матрицы, то получится 11 (поскольку 5 + 6 = 11). Такова же и сумма собственных значений (7 + 4 = 11); и это число противоположно первому из чисел, которые встречаются в характеристическом многочлене (−11 и 11 противоположны). Это очень важное число, называемое следом матрицы.
Характеристический многочлен, собственные значения, след — для чего все это? Видите ли, важность матриц не в них самих, а в том, что они представляют. Матричная арифметика, коль скоро вы ею овладели, — это просто набор технических навыков, как и в обычной арифметике. Но подобно тому, как обычные числа можно использовать для выражения гораздо более глубоких, более фундаментальных вещей, так же используются и матрицы. Прогулка от моего дома до Хантингтон-Вилидж занимает у меня 12 минут; расстояние составляет приблизительно 0,8 мили. Если начиная с завтрашнего утра Соединенные Штаты перейдут на метрическую систему, мне придется говорить «приблизительно 1,3 километра», а не «приблизительно 0,8 мили». Расстояние, однако, от этого не изменится; только числа, используемые для его выражения, пришлось бы изменить. Я по-прежнему проходил бы это расстояние за 12 минут (если только не состоится еще и переход к метрическим единицам времени).
Вот еще один пример: календарь, висящий у меня на стене, представляет собой численное выражение движений Солнца и Луны. Главным образом Солнца, поскольку у нас в Америке принят солнечный календарь, месяцы в котором рассинхронизированы с движением Луны. Однако этот календарь нам дали в соседнем китайском ресторане. Если присмотреться, то можно заметить, что там указаны месяцы и дни традиционного китайского лунного календаря, причем каждый месяц начинается в новолуние. Все числа отличаются от «солнечных» чисел, но они выражают те же небесные явления, то же течение времени, те же фактические моменты времени.
Точно так же обстоит дело и с матрицами. Великое значение матриц в том, что их можно использовать для представления и численного выражения некоторых более глубоких и более фундаментальных вещей. Что же это за вещи? Это операторы. Понятие оператора — одно из самых важных как в математике, так и в физике XX столетия. Я не собираюсь вдаваться в подробности насчет того, что же такое операторы, по крайней мере, до главы 20 точно не собираюсь. Важный момент, который надо осознать, — что это именно они притаились за всей этой суетой с матрицами и что именно их свойства мы и можем численно изучать, используя матрицы.
Теперь понятно, почему характеристический многочлен, собственные значения и след — понятия фундаментальные. Они суть свойства скрывающегося за матрицей оператора, а не матрицы самой по себе. На самом деле данный оператор можно представить многими матрицами, но это обязаны быть матрицы с одними и теми же собственными значениями. Приведенная выше (2×2)-матрица представляет некоторый оператор. Один и тот же оператор представляется и матрицей
 и матрицей
и матрицей
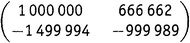 .
.
У всех этих матриц — и, конечно, еще у бесконечного числа матриц — один и тот же характеристический многочлен x2 − 11x + 28, одни и те же собственные значения 4 и 7 и один и тот же след 11. Это происходит просто потому, что такими свойствами обладает оператор.
Все это применимо к матрицам любого размера. Возьмем (4×4)-матрицу:

Ее характеристический многочлен равен x4 − 11x3 + 40x2 − 97x + 83. (Можно заметить, что след этой матрицы, как и след приведенной выше, равен 11. Это чистое совпадение, и эти матрицы больше никак не связаны.) Этот многочлен имеет полный набор из четырех нулей. С точностью до пяти знаков после запятой они равны 1,38087, 7,03608, 1,29152 − 2,62195i и 1,29152 + 2,62195i. Это, конечно, собственные значения матрицы. Два из них, как мы видим, являются комплексными числами (причем комплексно сопряженными друг другу, что всегда верно для многочлена с вещественными коэффициентами). Это вполне нормально, даже когда, как в данном случае, все числа в исходной матрице вещественные. Сумма четырех собственных значений равна 11 — мнимые компоненты сокращаются при сложении.
V.
После нескольких десятилетий исследований матриц математики расклассифицировали их на несколько различных типов. Они развили, так сказать, таксономию матриц, в которой полное семейство (N×N)-матриц — называемое математиками общей линейной группой порядка N и обозначаемое как GLN — было разбито на виды и рода.
Выберем всего один из видов в этом большом зверинце — эрмитовы матрицы, названные по имени великого французского математика Шарля Эрмита, с которым мы мельком встречались в главе 10.v. Числа, входящие в эрмитову матрицу, являются комплексными и организованы таким образом, что если число, стоящее в m-й строке и n-м столбце, есть a + bi, то число, стоящее в n-й строке и m-м столбце, есть a − bi. Другими словами, каждый элемент матрицы равен комплексному сопряжению (см. главу 11.v) своего отражения относительно главной диагонали. Попытаюсь прояснить это на примере эрмитовой (4×4)-матрицы:
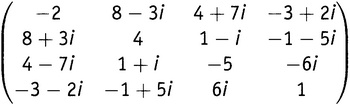
Как видно, элемент в третьей строке и первом столбце равен комплексному сопряжению элемента в первой строке и третьем столбце. Это эрмитова матрица. Заметим, что из определения следует, что все числа на главной диагонали должны быть вещественными, поскольку определение требует, чтобы каждое число на диагонали было комплексно сопряжено самому себе, а этим свойством обладают только вещественные числа: a + bi = a − bi, если и только если b = 0.



 и матрицей
и матрицей
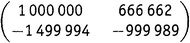 .
.