
Онлайн книга «Простая одержимость. Бернхард Риман и величайшая нерешенная проблема в математике»
| + | 0 | 1 | 2 | 3 | × | 0 | 1 | 2 | 3 | |
| 0 | 0 | 1 | 2 | 3 | 0 | 0 | 0 | 0 | 0 | |
| 1 | 1 | 0 | 3 | 2 | 1 | 0 | 1 | 2 | 3 | |
| 2 | 2 | 3 | 0 | 1 | 2 | 0 | 2 | 3 | 1 | |
| 3 | 3 | 2 | 1 | 0 | 3 | 0 | 3 | 1 | 2 |
Рисунок 17.2. Сложение и умножение в конечном поле F4.
Всякое поле, конечное или бесконечное, имеет важный параметр — число, называемое характеристикой. Характеристика поля говорит о том, сколько раз надо прибавить единицу к самой себе, чтобы получить нуль. Если 1 + 1 + 1 + … = 0 (где берется N слагаемых), то характеристика равна N. Понятно, что характеристика поля F2 равна 2. Чуть менее очевидно, хотя и без труда проверяется с помощью таблицы сложения на рисунке 17.2, то, что характеристика поля F4 тоже равна 2. Такие поля, как Q, R, С, в которых никакое прибавление единицы к самой себе какое угодно количество раз никогда не даст в результате нуль, по определению имеют характеристику «нуль». (Вы могли бы подумать, что более логичной будет характеристика «бесконечность», и вы, возможно, правы, но имеются веские причины и для того, чтобы объявить характеристику нулевой.) Можно проверить, что характеристика любого поля есть или нуль, или некоторое простое число.
Поскольку мы имеем дело с алгеброй, элементы полей не обязаны быть числами. Алгебра позволяет работать с математическими объектами любого типа. Рассмотрим все многочлены (полиномиальные функции) любой заданной степени, т.е. все выражения вида axn + bxn−1 + cxn−2 + …, где a, b, c и т.д. — целые числа. Теперь образуем множество всех рациональных функций, другими словами, функций, являющихся отношением (ratio) двух многочленов. Получим поле. Приведем пример сложения в этом поле:
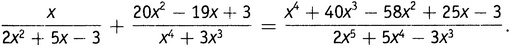
(Примерно этим и занимаются на уроках алгебры в старших классах.)
Коэффициенты многочленов не обязаны быть целыми. На самом деле можно позабавиться, сделав их элементами из конечного поля, такого как рассмотренное выше поле F2. В качестве примера сложения, которое при этом получается, имеем
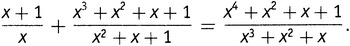
(При проверке этого равенства надо помнить, что в поле F2 выполнено 1 + 1 = 0, а потому x + x = 0, x2 − x2 = 0 и т.д.) Это поле будет называться полем рациональных функций над F2. В нем, разумеется, бесконечно много элементов; лишь коэффициенты ограничены своей принадлежностью к конечному полю. Таким образом, можно использовать конечное поле для построения бесконечного. Заметим еще, что, поскольку 1 + 1 = 0, это поле имеет характеристику 2. Следовательно, и бесконечные поля могут иметь конечную характеристику.
Не имеет особого смысла спрашивать, что собой представляет x в последних двух примерах. Это символ, для манипуляций с которым у нас имеются строго определенные правила. С алгебраической точки зрения главное в этом и состоит. На самом деле почти наверняка ответ на данный вопрос звучит как «x представляет собой число». Однако алгебраисты куда больше интересуются тем, какого типа это число — каким семействам, каким группам, каким полям оно принадлежит и какие правила манипуляций с ним выполнены. Для аналитика же наше число а + b√2 не слишком интересно. «Это просто вещественное число», — скажет аналитик. — «Ладно, алгебраическое число» (см. главу 11.ii), — если на него надавить. Но для алгебраиста, однако, оно представляет особый интерес постольку, поскольку относится к некоторому полю. Вообще алгебраисты и аналитики рассматривают не столько разные вещи, сколько аспекты одной и той же вещи. [159]{A8}
